Question

Let\[\Delta ABC \sim \Delta PQR\]. If area (ABC)\[ = 2.25{m^2}\], area (PQR)\[ = 6.25{m^2}\], PQ=0.5m, then length of AB is:
A.30 cm
B.0.5 m
C.50 cm
D.3 m

Answer 1

Hint: Ratio of areas of triangle is equal to the ratio of squares of the corresponding sides if the two triangles are similar. For two triangles to be similar the corresponding angles of the triangles must be equal, the corresponding sides of the triangles must be in the same ratio but they must not be necessarily of the same size.
In this question it is already said that the two triangles are similar triangles and their respective areas are given so by applying the ratio of area theorem we will find the missing side.

Complete step-by-step answer:
Given
\[\Delta ABC \sim \Delta PQR\]

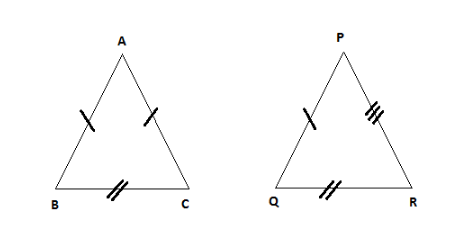
Since the two triangles ABC and PQR are similar so by applying the (SSS) property of the similar triangles we can write
\[\dfrac{{AB}}{{PQ}} = \dfrac{{BC}}{{QR}} = \dfrac{{CA}}{{RP}} - - (i)\]
Now the area of the two triangles are given which are in the ratio
\[\dfrac{{ar\left( {\Delta ABC} \right)}}{{ar\left( {\Delta PQR} \right)}} = \dfrac{{2.25}}{{6.25}} - - (ii)\]
Given length of the side \[PQ = 0.5m\]
Now we already know that ratio of areas of triangle is equal to the ratio of square of the corresponding sides so from equation (i) and (ii) for the length of the side AB we can write
\[\dfrac{{ar\left( {\Delta ABC} \right)}}{{ar\left( {\Delta PQR} \right)}} = {\left( {\dfrac{{AB}}{{PQ}}} \right)^2}\]
Hence by substituting the values we get
\[
\Rightarrow \dfrac{{2.25}}{{6.25}} = {\left( {\dfrac{{AB}}{{0.5}}} \right)^2} \\
\Rightarrow \sqrt {\dfrac{{225}}{{626}}} = \dfrac{{AB}}{{0.5}} \\
\Rightarrow \dfrac{{15}}{{25}} = \dfrac{{AB}}{{0.5}} \\
\Rightarrow AB = \dfrac{{15}}{{25}} \times 0.5 \\
   = 0.3m \;
 \]
Hence the length of the side AB is \[ = 0.3m = 0.3 \times 100 = 30cm\]
So, the correct answer is “Option A”.

Note: Students must note that the two triangles can be similar if any two corresponding angles of the two triangles are equal (AA) or if the three corresponding sides are in equal ratio (SSS) or if their two corresponding sides are in equal ratio and angles are equal (SAS)