Question

Let us assume that you make a plot on log-log paper of ${{V}_{rms}}$ ​versus $T$ for an ideal gas. (Alternatively, you could plot in ${{V}_{rms}}$​ versus $\ln T$ on ordinary graph paper). Represent that the plot is a straight line having slope $\dfrac{1}{2}$.

Answer 1

Hint: The rms velocity is found by taking the square root of the ratio of the thrice of the product of the universal gas constant and temperature to the mass of the gas. Take a log on both the sides and find the slope of the graph. This will help you in solving this question.

Complete step by step answer:
As we already know that the rms velocity is found by taking the square root of the ratio of the thrice of the product of the universal gas constant and temperature to the mass of the gas. This can be written as,
\[{{V}_{rms}}=\sqrt{\dfrac{3RT}{M}}\]
Do the log function on both the sides of the equation,
\[{{\log }_{e}}\left( {{V}_{rms}} \right)={{\log }_{e}}\left( \sqrt{\dfrac{3RT}{M}} \right)\]
This can be written as the sum like,
\[{{\log }_{e}}\left( {{V}_{rms}} \right)={{\log }_{e}}\left( \sqrt{T} \right)+{{\log }_{e}}\left( \sqrt{\dfrac{3R}{M}} \right)\]
The last term is a constant as all the terms in it are constant. Therefore we can write that,
\[{{\log }_{e}}\left( {{V}_{rms}} \right)=\dfrac{1}{2}{{\log }_{e}}\left({T} \right)+C\]
The general equation of the straight line graph can be shown as,
\[Y=mX+C\]
We can compare the both equations. Therefore we can find that,
\[\begin{align}
  & \text{intercept}\to \text{C} \\
 & \text{slope}=m\text{ }=\dfrac{1}{2} \\
\end{align}\]

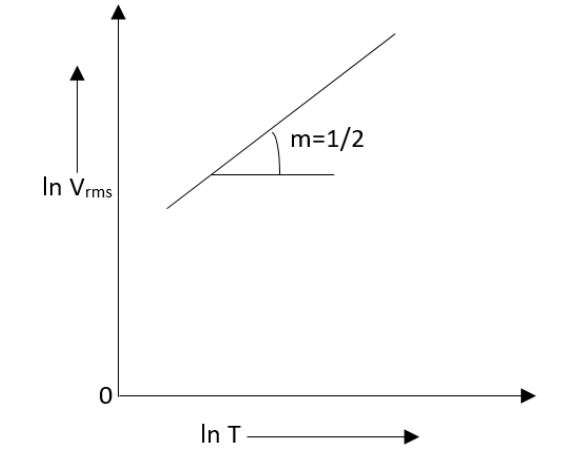
Therefore the graph will be a straight line with the slope mentioned as \[\dfrac{1}{2}\].
Hence the answer has been obtained.

Note: The rms velocity is the abbreviation of the root mean square velocity. It is defined as the square root of the mean of the square of the velocity. This velocity will be having the same units of velocity. This rms velocity has been used generally instead of the average velocity is that for a particular gas sample the resultant velocity is zero as the particles are moving in every direction.