Question

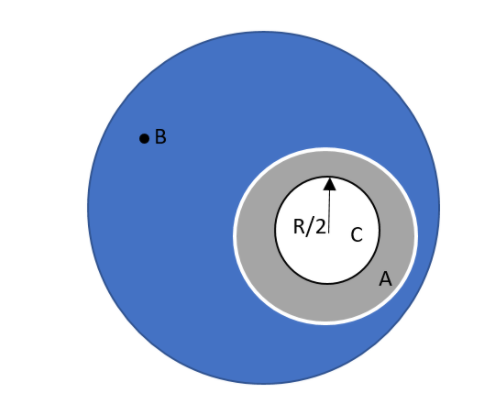
Let us assume that there is an air bubble of radius $\dfrac{R}{2}$​ inside the air cavity of radius $R$ inside a water drop of radius $3R$ as shown in the diagram. The ratio of gauge pressure at point C to gauge pressure at point B is given as,

$\begin{align}
  & A.4 \\
 & B.8 \\
 & C.12 \\
 & D.16 \\
\end{align}$

Answer 1

Hint: First of all find out the pressure at the point B. Then calculate the pressure at the point C. Take the difference between the pressure between the pressure at C and initial pressure. And also find out the difference between the pressure at B and the initial pressure. Take the ratio of them. This all will help you in answering this question.

Complete step by step answer:
The pressure at the point B is mentioned as,
${{P}_{B}}={{P}_{0}}+\dfrac{2T}{3R}$
Where ${{P}_{0}}$ be the initial pressure, $T$ be the tension of the water and $R$ be the radius of the air cavity.
The difference between the pressure B and the initial pressure can be written as,
${{P}_{B}}-{{P}_{0}}=\dfrac{2T}{3R}$
The pressure at the point C can be written as,
\[{{P}_{C}}={{P}_{0}}+\dfrac{2T}{3R}+\dfrac{2T}{R}+\dfrac{4T}{\dfrac{R}{2}}\]
Therefore the difference between the pressure C and the initial pressure can be written as,
\[{{P}_{C}}-{{P}_{0}}=\dfrac{2T}{3R}+\dfrac{2T}{R}+\dfrac{4T}{\dfrac{R}{2}}=\dfrac{32T}{3R}\]
Therefore the ratio of the gauge pressure at point C to the gauge pressure at the point C can be shown as,
\[\dfrac{{{P}_{C}}-{{P}_{0}}}{{{P}_{B}}-{{P}_{0}}}=16\]

So, the correct answer is “Option D”.

Note: Pressure can be measured by the analysis of an applied force by a fluid on a surface. Pressure is generally measured in the units of force per unit of surface area. So many methods have been created for the measurement of the pressure and vacuum. The gauge pressure is defined as the measure of the pressure calculated in a fluid is higher than that of the atmosphere.