Question

Let us assume that a yo-yo instead of rolling from rest, has been thrown so that the initial speed of the yo-yo down the string will be $1.3m{{s}^{-1}}$.How long will the yo-yo take to reach at the end of the string? When it reaches the end of the string, what will be the time taken?

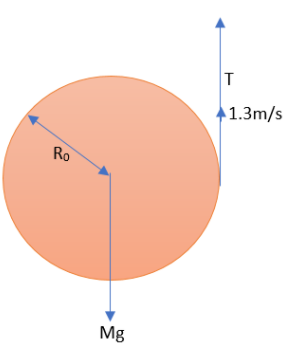
Where,
${{y}_{com}}=-1.2m$
${{I}_{com}}=0.000095kg{{m}^{2}}$
$M=0.12kg$
${{R}_{0}}=0.0032m$

Answer 1

Hint: The acceleration of the centre of mass can be found by taking the ratio of the acceleration due to gravity to the sum of one and ratio of the moment of inertia of the centre of mass to the product of the mass and the square of radius of the yo-yo. This will help you in answering this question.

Complete answer:
The acceleration of the centre of mass can be found by taking the ratio of the acceleration due to gravity to the sum of one and ratio of the moment of inertia of the centre of mass to the product of the mass and the square of radius of the yo-yo. This can be written as,
${{a}_{com}}=\dfrac{g}{1+\dfrac{{{I}_{com}}}{M{{R}_{0}}^{2}}}$
Where upward will be the positive translational direction. Taking the origin of the coordinate at the initial position which will lead to,
${{y}_{com}}={{v}_{0com}}+\dfrac{1}{2}{{a}_{0com}}{{t}^{2}}$
Substituting the values in this will give,
${{y}_{com}}={{v}_{0com}}+\dfrac{1}{2}\dfrac{g{{t}^{2}}}{1+\dfrac{{{I}_{com}}}{M{{R}_{0}}^{2}}}$
The y-coordinate of the centre of mass has been given as,
${{y}_{com}}=-1.2m$
Initial speed of the yo-yo will be,
${{v}_{0}}=-1.3m{{s}^{-1}}$
The moment of inertia of the centre of mass can be written as,
${{I}_{com}}=0.000095kg{{m}^{2}}$
The mass of the yo-yo will be,
$M=0.12kg$
The radius will be,
${{R}_{0}}=0.0032m$
The acceleration due to gravity can be shown as,
$g=9.8m{{s}^{-2}}$
Using the quadratic equation method, we can find the time. That is,
$\dfrac{\left( 1+\dfrac{{{I}_{com}}}{M{{R}_{0}}^{2}} \right)\left( {{v}_{com,0}}\pm \sqrt{{{v}^{2}}_{com,0}-\dfrac{2g{{y}_{com}}}{1+\dfrac{{{I}_{com}}}{M{{R}_{0}}^{2}}}} \right)}{g}$
Substituting the values in the equation can be shown as,
\[t=\dfrac{\left( 1+\dfrac{0.000095}{\left( 0.12 \right){{\left( 0.0032 \right)}^{2}}} \right)\left( -1.3\pm \sqrt{{{\left( 1.3 \right)}^{2}}-\dfrac{2\times 9.8\times -1.2}{1+\dfrac{0.000095}{0.12\times {{\left( 0.0032 \right)}^{2}}}}} \right)}{9.8}\]
Simplifying this equation will give,
$t=-21.7\text{ or }0.885$
Here we can choose $t=0.89s$ as the correct answer.

Note:
The acceleration can be defined as the rate of variation of the velocity with respect to the time taken. The velocity can be defined as the rate of variation of the displacement of a body with respect to the time taken centre of mass is an imaginary point where the whole mass of the body is considered to be concentrated.