Question

Let us assume that a particle of mass $2m$ is being projected at an angle of \[45{}^\circ \] with horizontal velocity of \[20\sqrt{2}m{{s}^{-1}}\]. After \[1s\], an explosion takes place and the particle is cracked into two equal pieces. Because of the explosion one part will come to rest. What will be the maximum height reached by the other part. Take \[g=10m{{s}^{-2}}\],
\[\begin{align}
  & A.50m \\
 & B.25m \\
 & C.40m \\
 & D.35m \\
\end{align}\]

Answer 1

Hint: Find the height moved by the particle in one second. Find the velocity of the particle after one second and the angle with the horizontal is to be calculated. The initial and final velocities of the particle is to be found. And the final height will be found by the equation of maximum height. Total height will be the sum of both the heights.

Complete step by step solution:

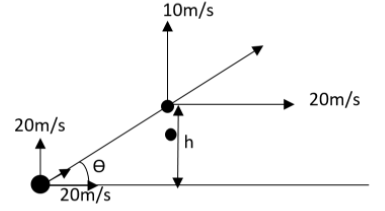
The height moved by the particle in \[1s\]can be found by the equation,
\[h=ut+\dfrac{1}{2}g{{t}^{2}}\]
As mentioned in the question,
The initial velocity can be shown as,
\[u=20m{{s}^{-1}}\]
The time taken will be written as,
\[t=1s\]
And the acceleration due to gravity will be,
\[g=10m{{s}^{-2}}\]
Substituting the values in it will give,
\[h=20\times 1+\dfrac{1}{2}\times 10\times {{1}^{2}}=15m\]
After one second, the vertical speed will become \[v\]. Let us perform newton’s first equation of motion.
That is,
\[v-u=-gt\]
Substituting the values in it,
\[\begin{align}
  & v-20=-10\times 1 \\
 & v=10m{{s}^{-1}} \\
\end{align}\]
The angle \[\theta \] at a height \[h\] with the horizontal can be written as,
\[\begin{align}
  & \tan \theta =\dfrac{10}{20}=\dfrac{1}{2} \\
 & \sin \theta =\dfrac{1}{\sqrt{5}} \\
\end{align}\]
Before the explosion, the velocity of the particle will be,
\[{{v}_{e}}=\sqrt{{{10}^{2}}+{{20}^{2}}}=\sqrt{500}=10\sqrt{5}\]
And after the explosion the mass of the particle becomes half of the original value.
Therefore in accordance with conservation of momentum, the velocity will become twice. That is,
\[{{v}_{e}}^{\prime }=20\sqrt{5}\]
The height travelled after explosion will be found as,
\[{h}'=\dfrac{{{\left( {{v}_{e}}^{\prime } \right)}^{2}}{{\sin }^{2}}\theta }{2g}\]
Substituting the values in it will give,
\[{h}'=\dfrac{{{\left( 20\sqrt{5} \right)}^{2}}\times \dfrac{1}{5}}{2\times 10}=20cm\]
Hence the total height will be the sum of both the heights.
That is,
\[H=20+15=35cm\]

The answer has been mentioned as option D.

Note:
The conservation law of momentum says that the total momentum of a body before and after a collision will be similar. The initial momentum of the body before the collision will be the same as the final momentum of the body after the collision. Momentum is a vector quantity having both direction as well as magnitude.