Question

Let TP and TQ are tangents to the parabola, ${{y}^{2}}=4ax$ at P and Q. If the chord PQ passes through a fixed point (-a, b), then find the locus of T?

Answer 1

Hint: Suppose point T as $\left( {{h}_{1}}k \right)$or use any other variables. Equation of chord of contact by joining the point of tangency with the help of two tangents drawn from point T, is given by the equation
T = 0
Where, we need to replace
$\begin{align}
  & {{x}^{2}}\to hx,{{y}^{2}}\to ky \\
 & x\to \dfrac{x+h}{2},y\to \dfrac{y+k}{2} \\
\end{align}$ , from the equation of curve. Hence, use the given condition to get the solution (locus of point T).

Complete step by step answer:
As we know ${{y}^{2}}=4ax$ is a parabola with vertex at (o, o) and symmetric about x-axis. Here, it is given that TP and TQ are tangents to the parabola ${{y}^{2}}=4ax$at P and Q and hence, we need to determine the locus of T, if the chord PQ passes through a fixed point (-a, b).
Hence, diagram with the help of above information is given as

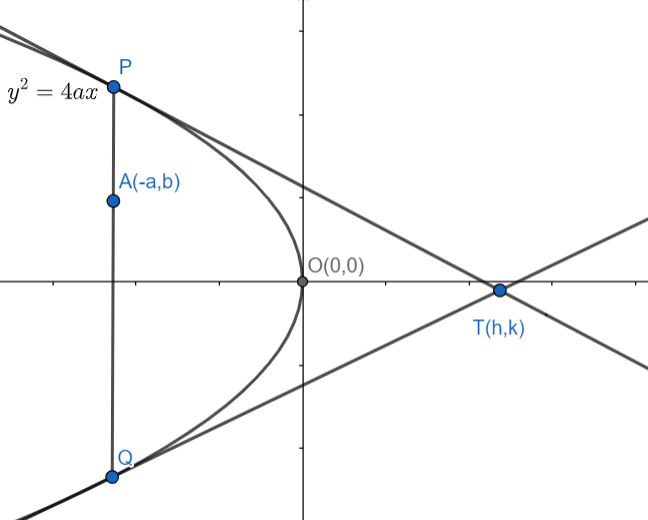
Let us suppose the coordinates of point T is $\left( {{h}_{1}}k \right)$. Now, as we know the chord of contact for any conic ‘s’ from the point $\left( {{x}_{1}},{{y}_{1}} \right)$ by which tangents are drawn to the parabola. Hence, chord of contact by joining those contacts of tangency is given as:
T = 0 ………………(i)
Where, we need to replace the terms of conic as
$\begin{align}
  & {{x}^{2}}\to x{{x}_{1}} \\
 & {{y}^{2}}\to y{{y}_{1}} \\
 & x\to \dfrac{x+{{x}_{1}}}{2} \\
 & y\to \dfrac{y+{{y}_{1}}}{2} \\
\end{align}$
Hence, chord of contact can be given with the help of curve ${{y}^{2}}=4ax$ad point T$\left( {{h}_{1}}k \right)$ is
$ky=4a\dfrac{\left( x+h \right)}{2}$
$ky=2a\left( x+h \right)$…………………..(ii)
Now, it is given that the chord of contact i.e. PQ is passing through the point (-a, b). It means the equation (ii) will satisfy x = -a, y = b. so, we get
bk = 2a(-a + h)
Now, replace $\left( {{h}_{1}}k \right)\to \left( {{x}_{1}},{{y}_{1}} \right)$to get the required locus.
by = 2a(x – a) …………………(iii)

Hence, equation (iii) represents the locus of point T.

Note: Using the direct results in conic sections always make the solution flexible and less time taking. And the equation T = 0 for writing the equation of chord of contact from a point$\left( {{h}_{1}}k \right)$can be proved by taking two parametric coordinates$\left( a{{t}^{2}},2a{{t}_{1}} \right),\left( a{{t}^{2}}_{2},2a{{t}_{2}} \right)$.
 Calculate equation of chord with the help of these two points. Get the equations of tangent through both the points $\left( a{{t}^{2}}_{1},2a{{t}_{1}} \right),\left( a{{t}^{2}}_{2},2a{{t}_{2}} \right),$and hence, solve them to relate the equation with the intersecting points of tangents. So, it would be unnecessary to solve these parts in the problem. Hence, one may remember the results in conic sections and will definitely help in these kinds of questions.
Understanding these questions with the help of drawing a diagram is also a key point of the question. So, try to focus on words as well and draw the suitable diagram to visualize the problem.