Question

Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that \[\angle ABC\] is equal to half the difference of the angles subtended by the chord’s AC and DE at the centre.

Answer 1

Hint: First of all, draw the figure of the circle which will give us an idea of what we have to find and join the lines AC and DE. Then solve the problem by angle sum property of the triangle and the quadrilateral formed. So, use this concept to reach the solution of the given problem.

Complete step-by-step answer:

Given chords AD and CE are equal.

Here we have to prove \[\angle ABC = \dfrac{1}{2}\left( {\angle AOC - \angle DOE} \right)\].

Join AC and DE as shown in the below figure:

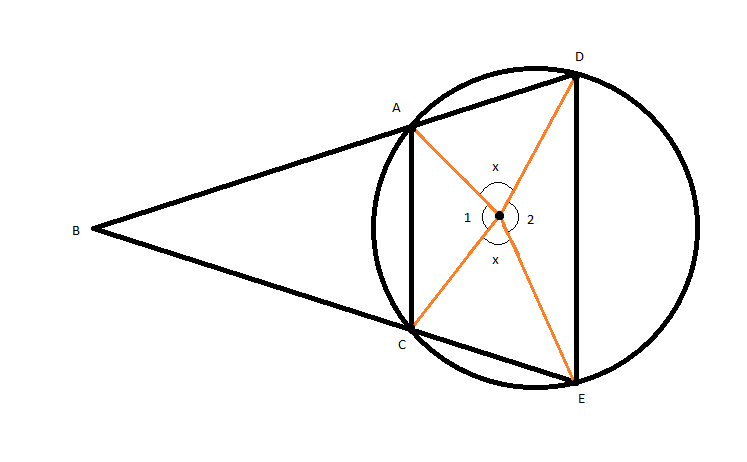
Given

AD = CE

\[\therefore \angle AOD = \angle COE{\text{ }}\left( {{\text{Equal chords subtend equal angle at the center}}} \right)\]

Let \[\angle AOD = \angle COE = x\]

Now, around point O,

Sum of angles around a point \[ = {360^0}\]

\[

  \angle 1 + \angle 2 + \angle AOD + \angle COE = {360^0} \\

  \left( {\angle 1 + \angle 2} \right) + x + x = {360^0} \\

  2x = {360^0} - \left( {\angle 1 + \angle 2} \right) \\

  x = \dfrac{{{{360}^0}}}{2} - \dfrac{{\left( {\angle 1 + \angle 2} \right)}}{2} \\

  \therefore x = {180^0} - \dfrac{{\left( {\angle 1 + \angle 2}
\right)}}{2}............................................................\left( 1 \right) \\

\]

Now, in \[\Delta COE\]

\[

  OC = OE{\text{ }}\left( {{\text{Both are radius}}} \right) \\

  \angle OEC = \angle OCE{\text{ }}\left( {{\text{Angles opposite to equal sides of a triangle are equal}}} \right) \\

\]

In \[\Delta COE\],

\[

  \angle COE + \angle OCE + \angle OEC = {180^0}{\text{ }}\left( {{\text{Angle sum property}}} \right) \\

  x + \angle OCE + \angle OCE = {180^0}{\text{ }}\left( {{\text{As }}\angle OCE = \angle OEC} \right) \\

  x + 2\angle OCE = {180^0} \\

  \angle OCE = \dfrac{{{{180}^0}}}{2} - \dfrac{x}{2} \\

  \angle OCE = {90^0} - \dfrac{x}{2} \\

\]

Similarly, we have

\[\angle OAD = {90^0} - \dfrac{x}{2}\]

Now, for line BE

\[

  \angle BCO + \angle OCE = {180^0}{\text{ }}\left( {{\text{Linear pair}}}
\right) \\

  \angle BCO = {180^0} - \angle OCE \\

  \angle BCO = {180^0} - \left( {{{90}^0} - \dfrac{x}{2}} \right) \\

  \angle BCO = {90^0} + \dfrac{x}{2} \\

\]

Similarly, we have

\[\angle BAO = {90^0} + \dfrac{x}{2}\]

Now, in quadrilateral ABCO,

\[

  \angle B + \angle BCO + \angle BAO + \angle 1 = {360^0} \\

  \angle B + {90^0} + \dfrac{x}{2} + {90^0} + \dfrac{x}{2} + \angle 1 = {360^0} \\

  \angle B + {180^0} + {180^0} - \dfrac{1}{2}\left( {\angle 1 + \angle 2} \right) + \angle 1 =
{360^0}{\text{ }}\left( {{\text{From }}\left( 1 \right)} \right) \\

  \angle B + {360^0} - \dfrac{1}{2}\angle 1 - \dfrac{1}{2}\angle 2 + \angle 1 = {360^0} \\

  \angle B + \dfrac{1}{2}\angle 1 - \dfrac{1}{2}\angle 2 = {360^0} - {360^0} = 0 \\

  \angle B = \dfrac{1}{2}\angle 1 - \dfrac{1}{2}\angle 2 \\

  \angle B = \dfrac{1}{2}\left( {\angle 1 - \angle 2} \right) \\

\]

As \[\angle ABC = \angle B,\angle AOC = \angle 1{\text{ and }}\angle DOE = \angle 2\], we
have

\[\therefore \angle ABC = \dfrac{1}{2}\left( {\angle AOC - \angle DOE} \right)\]

Hence proved.

Note: The sum of the angles in a triangle is equal to \[{180^0}\] and the sum of angles in a quadrilateral is equal to \[{360^0}\]. Equal chords in a circle subtends equal angles at the centre of the circle. Angles opposite to equal sides of a triangle are equal.