Question

Let the tangents PA and PB are drawn from P(0,-2) to the circle ${{x}^{2}}+{{y}^{2}}+2x-4y=0$. The area of the triangle PAB is
[a] $\dfrac{2\sqrt{15}}{17}$
[b] $\dfrac{4\sqrt{15}}{\sqrt{17}}$
[c] $\dfrac{24\sqrt{15}}{17}$
[d] $\dfrac{24\sqrt{15}}{\sqrt{17}}$

Answer 1

Hint: Use the fact that the equation of the chord of contact of tangents of the circle ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ from the point $P\left( {{x}_{1}},{{y}_{1}} \right)$ is given by $x{{x}_{1}}+y{{y}_{1}}+g\left( x+{{x}_{1}} \right)+f\left( y+{{y}_{1}} \right)+c=0$. Solve the equation of the chord of contact and the circle and hence find the coordinates of A and B. Use the fact that the area of the triangle formed by the points $A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right),C\left( {{x}_{3}},{{y}_{3}} \right)$ is given by $\Delta =\dfrac{1}{2}\left| \begin{matrix}
   {{x}_{1}} & {{y}_{1}} & 1 \\
   {{x}_{2}} & {{y}_{2}} & 1 \\
   {{x}_{3}} & {{y}_{3}} & 1 \\
\end{matrix} \right|$
. Hence find the area of the triangle PAB.

Complete step by step answer:

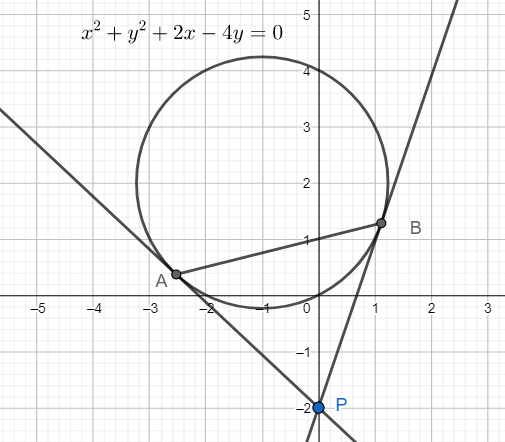
Equation of the circle is ${{x}^{2}}+{{y}^{2}}+2x-4y=0$
We know that the equation of the chord of contact of the tangents of the circle ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ from the point $P\left( {{x}_{1}},{{y}_{1}} \right)$ is given by $x{{x}_{1}}+y{{y}_{1}}+\left( x+{{x}_{1}} \right)+f\left( y+{{y}_{1}} \right)+c=0$
Hence the equation of AB is
$\begin{align}
  & x\left( 0 \right)+y\left( -2 \right)+\left( x+0 \right)-2\left( y-2 \right)=0 \\
 & x-4y+4=0 \\
 & \Rightarrow x=4y-4 \\
\end{align}$
Substituting the value of x in the equation of the circle, we get
$\begin{align}
  & {{\left( 4y-4 \right)}^{2}}+{{y}^{2}}+2\left( 4y-4 \right)-4y=0 \\
 & \Rightarrow 16{{y}^{2}}+16-32y+{{y}^{2}}+8y-8-4y=0 \\
 & \Rightarrow 17{{y}^{2}}-28y+8=0 \\
\end{align}$
Let the roots of this expression be ${{y}_{1}},{{y}_{2}}$
Hence, we have ${{y}_{1}}+{{y}_{2}}=\dfrac{28}{17},{{y}_{1}}{{y}_{2}}=\dfrac{8}{17}$
Also, we have $A\equiv \left( 4{{y}_{1}}-4,{{y}_{1}} \right),B\equiv \left( 4{{y}_{2}}-4,{{y}_{2}} \right)$
We know that the area of the triangle $\Delta ABC$ formed by the points $A\left( {{x}_{,1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right),C\left( {{x}_{3}},{{y}_{3}} \right)$ is given by $\Delta =\dfrac{1}{2}\left| \begin{matrix}
   {{x}_{1}} & {{y}_{1}} & 1 \\
   {{x}_{2}} & {{y}_{2}} & 1 \\
   {{x}_{3}} & {{y}_{3}} & 1 \\
\end{matrix} \right|$ which we expand by row operations and third column to have $\Delta =\dfrac{1}{2}\left| \begin{matrix}
   {{x}_{2}}-{{x}_{1}} & {{y}_{2}}-{{y}_{1}} \\
   {{x}_{3}}-{{x}_{1}} & {{y}_{3}}-{{y}_{1}} \\
\end{matrix} \right|$
Hence, we have
$ar\left( \Delta PAB \right)=\dfrac{1}{2}\left| \begin{matrix}
   4{{y}_{1}}-4-0 & {{y}_{1}}+2 \\
   4{{y}_{2}}-4-0 & {{y}_{2}}+2 \\
\end{matrix} \right|$
Hence, we have
\[ar\left( \Delta PAB \right)=\dfrac{1}{2}\left| \left( 4{{y}_{1}}-4 \right)\left( {{y}_{2}}+2 \right)-\left( 4{{y}_{2}}-4 \right)\left( {{y}_{1}}+2 \right) \right|\]
Taking 4 common inside modulus sign, we get
$ar\left( \Delta PAB \right)=2\left| \left( {{y}_{1}}-1 \right)\left( {{y}_{2}}+2 \right)-\left( {{y}_{2}}-1 \right)\left( {{y}_{1}}+2 \right) \right|$
Expanding the terms inside the modulus sign, we get
$\begin{align}
  & ar\left( \Delta PAB \right)=2\left| {{y}_{1}}{{y}_{2}}+2{{y}_{1}}-{{y}_{2}}-2-{{y}_{1}}{{y}_{2}}-2{{y}_{2}}+{{y}_{1}}+2 \right| \\
 & =6\left| {{y}_{1}}-{{y}_{2}} \right| \\
\end{align}$
We know that ${{\left( a-b \right)}^{2}}={{\left( a+b \right)}^{2}}-4ab$
Hence, we have
${{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}={{\left( {{y}_{1}}+{{y}_{2}} \right)}^{2}}-4{{y}_{1}}{{y}_{2}}=\dfrac{{{28}^{2}}}{{{17}^{2}}}-\dfrac{32}{17}=\dfrac{{{28}^{2}}-17\times 32}{{{17}^{2}}}=\dfrac{240}{{{17}^{2}}}$
Taking square root on both sides, we get
$\left| {{y}_{1}}-{{y}_{2}} \right|=\dfrac{4\sqrt{15}}{17}$
Hence, we have
$ar\left( \Delta PAB \right)=6\left( \dfrac{4\sqrt{15}}{17} \right)=\dfrac{24\sqrt{15}}{17}$

So, the correct answer is “Option c”.

Note: [1] This question can also be solved directly using Pythagoras theorem and trigonometry without the use of analytical geometry. However the calculations will be more tedious to perform. Hence the method should be avoided as it is more prone to calculation mistakes.