Question

Let the tangent at point P of the curve ${{x}^{2m}}{{y}^{\dfrac{n}{2}}}={{a}^{\dfrac{4m+n}{2}}}$ meets the x-axis and the y-axis at A and B, respectively. If $AP:PB=\dfrac{n}{\lambda m}$, where P lies between A and B, then find the value of $\lambda $
[a] 4
[b] 3
[c] -4
[d] -3

Answer 1

Hint: Take logarithm on both sides of the equation and differentiate with respect to x, Hence find the expression for $\dfrac{dy}{dx}$. Hence find the slope of the tangent at a point $P\left( {{x}_{1}},{{y}_{1}} \right)$ on the given curve and hence find the equation of the tangent. Determine the coordinates of points of intersection of the tangent with the axis. Hence determine the ratio in which P divides AB.
Alternatively form the equation of the family of the curves whose tangent at point P meets x-axis at A and B and satisfies AP: PB $=\dfrac{n}{\lambda m}$. Solve the differential equation and compare with the given equation. Hence find the value of $\lambda $.

Complete step-by-step answer:

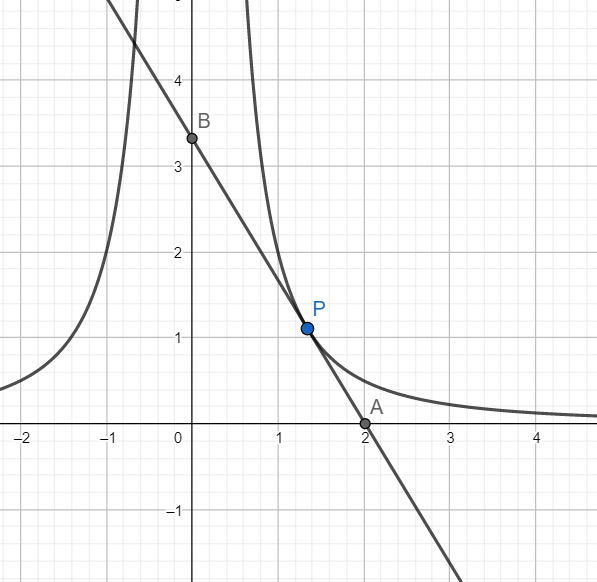
We have ${{x}^{2m}}{{y}^{\dfrac{n}{2}}}={{a}^{\dfrac{4m+n}{2}}}$
Taking log on both sides, we get
$\log \left( {{x}^{2m}}{{y}^{\dfrac{n}{2}}} \right)=\log \left( {{a}^{\dfrac{4m+n}{2}}} \right)$
Using $\log mn=\log m+\log n$ and $\log \left( {{a}^{n}} \right)=n\log a$, we get
$2m\log x+\dfrac{n}{2}\log y=\dfrac{4m+n}{2}\log a$
Differentiating both sides of the equation, we get
$2m\dfrac{1}{x}+\dfrac{n}{2}\dfrac{1}{y}\dfrac{dy}{dx}=0$
Subtracting $\dfrac{2m}{x}$ from both sides of the equation, we get
$\dfrac{n}{2y}\dfrac{dy}{dx}=\dfrac{-2m}{x}$
Multiplying both sides of the equation by $\dfrac{2y}{n}$, we get
$\dfrac{dy}{dx}=\dfrac{-4my}{nx}$
Hence the slope of the tangent at $\text{ }P\left( {{x}_{1}},{{ y }_{1}} \right)$ is given by $m={{\left. \dfrac{dy}{dx} \right|}_{x={{x}_{1}},y={{ y }_{1}}}}=\dfrac{-4m{{y}_{1}}}{n{{x}_{1}}}$
Hence the equation of the tangent is given by
$y-{{y}_{1}}=\dfrac{-4m{{y}_{1}}}{n{{x}_{1}}}\left( x-{{x}_{1}} \right)$
At point A, we have y = 0
Hence, we have
$\begin{align}
  & -{{y}_{1}}=\dfrac{-4m{{y}_{1}}}{n{{x}_{1}}}\left( x-{{x}_{1}} \right) \\
 & \Rightarrow n{{x}_{1}}=4m\left( x-{{x}_{1}} \right) \\
\end{align}$
Dividing both sides by 4m, we get
$x-{{x}_{1}}=\dfrac{n{{x}_{1}}}{4m}$
Adding ${{x}_{1}}$ on both sides, we get
$x=\dfrac{n+4m}{4m}{{x}_{1}}$
At point B, we have x=0.
Hence, we have
$y-{{y}_{1}}=\dfrac{-4m{{y}_{1}}}{n{{x}_{1}}}\left( -{{x}_{1}} \right)=\dfrac{4m{{y}_{1}}}{n}$
Adding ${{y}_{1}}$ on both sides of the equation, we get
$y=\left( \dfrac{4m}{n}+1 \right){{y}_{1}}=\dfrac{4m+n}{n}{{y}_{1}}$
Let P divides AB in the ratio of $k:1$
Hence, we have
$P\equiv \left( \dfrac{k\times 0+\dfrac{4m+n}{4m}{{x}_{1}}}{k+1},\dfrac{k\times \dfrac{4m+n}{n}{{y}_{1}}}{k+1} \right)$
But $\text{ }P\equiv \left({{ x }_{1}},{{y}_{1}} \right)$
Hence, we have
$\dfrac{4m+n}{4m\left( k+1 \right)}=1$
Multiplying both sides by k+1, we get
$k+1=\dfrac{4m+n}{4m}$
Subtracting 1 from both sides, we get
$k=\dfrac{4m+n}{4m}-1=\dfrac{n}{4m}$
Hence the ratio in which P divides AB is $\dfrac{n}{4m}$
Hence $\lambda =4$
Hence option [a] is correct

So, the correct answer is “Option [a]”.

Note: Alternative Method: Best method
Equation of the tangent at point $P\left( x,y \right)$ is given by
$Y-y=\dfrac{dy}{dx}\left( X-x \right)$
At point A, we have Y = 0
Hence $-y=\dfrac{dy}{dx}\left( X-x \right)$
Hence, we have
$X=x+\dfrac{-y}{\dfrac{dy}{dx}}$
Since P divides AB in the ratio $\dfrac{n}{\lambda m}$, we have
$x=\dfrac{\lambda m\left( x-\dfrac{y}{\dfrac{dy}{dx}} \right)}{n+\lambda m}$
Multiplying both sides by $n+\lambda m$, we get
$\left( n+\lambda m \right)x=\lambda m\left( x-\dfrac{y}{\dfrac{dy}{dx}} \right)$
Dividing both sides by$\lambda m$ , we get
$\dfrac{n+\lambda m}{\lambda m}x=x-\dfrac{y}{\dfrac{dy}{dx}}$
Subtracting x from both sides, we get
$\begin{align}
  & \dfrac{n}{\lambda m}x=-\dfrac{y}{\dfrac{dy}{dx}} \\
 & \Rightarrow \dfrac{n}{\lambda m}x=-y\dfrac{dx}{dy} \\
 & \Rightarrow \dfrac{dy}{y}=-\dfrac{\lambda m}{n}\dfrac{dx}{x} \\
\end{align}$
Integrating both sides, we get
$\log y=-\dfrac{\lambda m}{n}\log x+\log C$
Hence, we have
$\log \left( y{{x}^{\dfrac{\lambda m}{n}}} \right)=\log C$
Hence, we have
$y{{x}^{\dfrac{\lambda m}{n}}}=C$
Raising power to $\dfrac{n}{2}$ on both sides of the equation, we get
${{y}^{\dfrac{n}{2}}}{{x}^{\dfrac{\lambda m}{2}}}={{C}^{\dfrac{n}{2}}}=C'$
Comparing the equation, with the given equation, we get
$\begin{align}
  & \dfrac{\lambda }{2}=2 \\
 & \Rightarrow \lambda =4 \\
\end{align}$
Hence, the value of $\lambda $ is 4