Question

Let the point B be the reflection of the point A(2, 3) with respect to the line 8x-6y-23=0. Let ${{T}_{A}}\text{ and }{{T}_{B}}$ be circles of radii 2 and 1 with centers A and B respectively. Let T be a common tangent to the circles ${{T}_{A}}\text{ and }{{T}_{B}}$ such that both the circles are on the same side of T. If C is the point of intersection of T and the line passing through A and B then the length of the line segment AC is ..

Answer 1

Hint: First of all we will draw figure of given arrangements, then we will assume an angle at point C and try to calculate $\sin \theta $ using formula \[\sin \theta =\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}\]. Also, as radius and tangent at a point on a circle are perpendicular so $\sin \theta $ formula is applicable as the triangle becomes right angled.
After calculating $\sin \theta $ between two triangles of two circle ${{T}_{A}}\text{ and }{{T}_{B}}$ we will calculate the distance between a point and a line, using formula \[d=\dfrac{\left| a{{x}_{0}}+b{{y}_{0}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\]
Where line is $ax+by+c=0$ and point is $P\left( {{x}_{0}},{{y}_{0}} \right)$

Complete step-by-step answer:
Let us first form a figure for the given condition, we have a line $8x-6y-23=0$
A point B which is reflection of the point A (2, 3) with respect to line $8x-6y-23=0$
${{T}_{A}}:$ A circle at point B as center of radius 2.
${{T}_{B}}:$ Another circle at point B as center of radius 1.
T is a common tangent of ${{T}_{A}}\text{ and }{{T}_{B}}$ and both the circles have T on the same side.
C = is the point of intersection of T to line AB.

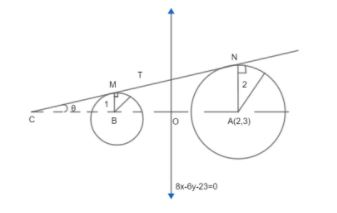
Let us assume $\angle TCB=\theta $ and a point M on circle ${{T}_{B}}$ such that MB = 1 and a point N on circle ${{T}_{A}}$ such that AN = 2.
Now, because in a circle the radius and tangent at a same point is perpendicular $\angle CMB={{90}^{\circ }}$
This is so as;
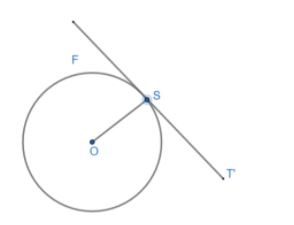
If a circle F is given as below having O as center a point S is taken on circumference of circle and OS = radius. Then, if a tangent T' is drawn at point S; then radius OS and tangent T' are perpendicular to each other,

Applying this theory, we have in $\Delta CBM;\angle CMB={{90}^{\circ }}$
Hence, $\Delta CBM$ is a right angled triangle.
Now, we will calculate $\sin \theta $ in $\Delta CBM$
To do so, use the formula of $\sin \theta $ stated as below,
If ABC is a right angled triangle, right angled at B and $\angle ACB=\theta $ then

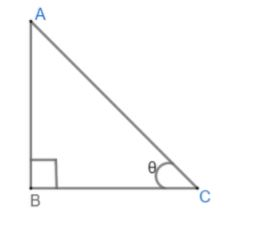
\[\begin{align}
  & \sin \theta =\dfrac{\text{Perpendicular}}{\text{Hypotenuse}} \\
 & \Rightarrow \sin \theta =\dfrac{\text{AB}}{\text{AC}} \\
\end{align}\]
Using this formula of $\sin \theta $ in $\Delta CBM$ we have
\[\sin \theta =\dfrac{BM}{CB}\]
We had BM = radius of ${{T}_{B}}=1$
\[\Rightarrow \sin \theta =\dfrac{1}{CB}\text{ }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. (i)}\]
Now, similarly consider $\Delta CNA;\angle NCA=\theta $
NA = radius of ${{T}_{A}}=2\text{ and }\angle CNA={{90}^{\circ }}$
By using the theory stated above that, radius and tangent at a point on a circle is perpendicular. Now, we will use formula of $\sin \theta $ stated above
\[\begin{align}
  & \sin \theta =\dfrac{AN}{CA}\text{ and AN=2} \\
 & \Rightarrow \sin \theta =\dfrac{2}{CA}\text{ }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. (ii)} \\
\end{align}\]
From equation (i) and (ii) we see
\[\begin{align}
  & \Rightarrow \dfrac{1}{CB}=\sin \theta =\dfrac{2}{CA} \\
 & \Rightarrow \dfrac{1}{CB}=\dfrac{2}{CA} \\
\end{align}\]
Multiplying by CA we get:
\[\Rightarrow \dfrac{CA}{CB}=2\]
Taking reciprocal:
\[\Rightarrow \dfrac{CB}{CA}=\dfrac{1}{2}\]
Now from figure CB = CA - BA substituting this, we get:
\[\begin{align}
  & \Rightarrow \dfrac{CB}{CA}=\dfrac{1}{2} \\
 & \Rightarrow \dfrac{CA-BA}{CA}=\dfrac{1}{2}\text{ }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. }\text{. (iii)} \\
\end{align}\]
Now, because B is reflection of A about line $O=8x-6y-23=0$ so we have:
\[\begin{align}
  & OA=OB \\
 & \text{also }AB=OA+OB \\
 & \text{But }OA=OB \\
 & \Rightarrow AB=OA+OA \\
 & \Rightarrow AB=2\left( OA \right) \\
\end{align}\]
Now, we will calculate the value of OA.
For that, we will use the formula of shortest distance of a point from a line.
If we have point $P\left( {{x}_{0}},{{y}_{0}} \right)$ and line $L=ax+by+c=0$ then distance d:
\[d=\dfrac{\left| a{{x}_{0}}+b{{y}_{0}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\]
Using this formula, to find distance DA where we have A = (2, 3) and line $O=8x-6y-23=0$
\[\begin{align}
  & \text{Distance OA}=\dfrac{\left| 8\times 2-6\times 3-23 \right|}{\sqrt{{{8}^{2}}+{{6}^{2}}}} \\
 & OA=\dfrac{\left| 16-18-23 \right|}{\sqrt{64+36}} \\
 & OA=\dfrac{\left| -25 \right|}{\sqrt{100}} \\
 & OA=\dfrac{25}{10}=\dfrac{5}{2} \\
 & \Rightarrow OA=\dfrac{5}{2} \\
\end{align}\]
Now, \[AB=2\left( OA \right)\Rightarrow AB=2\times \dfrac{5}{2}=5\]
Using value of AB in equation (iii) we get:
\[\dfrac{CA-5}{CA}=\dfrac{1}{2}\]
Cross multiplying:
\[\begin{align}
  & 2\left( CA-5 \right)=CA \\
 & 2CA-CA=10 \\
 & CA=10 \\
\end{align}\]
Therefore, the length of side AC is 10, which is our required answer.

Note: While calculating $\sin \theta $ we can also go for calculating $\cos \theta $ using formula of cos in a right angled triangle given as $\cos \theta =\dfrac{\text{Base}}{\text{Hypotenuse}}$ then using \[\cos \theta =\sqrt{1-{{\sin }^{2}}\theta }\] to calculate $\sin \theta $. But this would make the solution longer and increase chances of mistake, so this step should be avoided.
One major key point while calculating distance between point and line is that we have a formula for shortest distance and perpendicular line is shortest distance, so anyway this formula is applicable here.