Question

Let the cost of a pen and a pencil be Rs x and Rs y respectively. Anuj pays Rs 34 for 3 pens and 2 pencils. Write the given data in the form of a linear equation in two variables. Also represent it graphically.

Answer 1

Hint: To solve this question, we need to see that each pen cost Rs x and each pencil costs Rs y. So, when we multiply with the number of the quantity of price of each pen and pencil, that will be equal to the final amount paid.

Complete step by step solution:
Given, the cost of a pen and a pencil be Rs x and Rs y respectively.
If Anuj pays Rs 34 for 3 pens and 2 pencils.
We need to form the linear equation in two variables.
The price paid for 3 pens will be equal to 3x.
The price paid for 2 pencils will be equal to 2y.
As, it is mentioned in the question that Anuj pays Rs 34.
Therefore, \[3x + 2y = 34\].
This the linear equation in two variables.
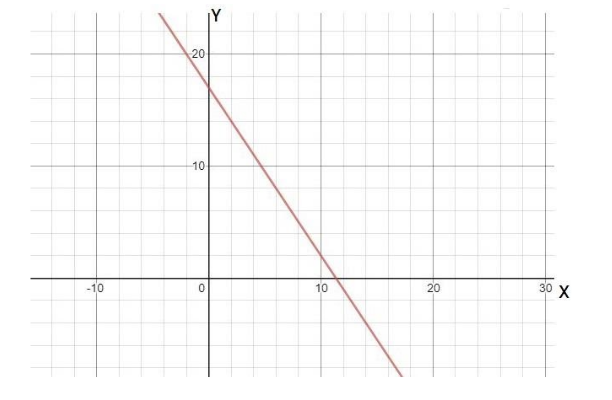
To represent it graphically, we need to find the y-intercept and the x-intercept of the line.
First, put the value of x as zero and find the value of y, from the equation \[3x + 2y = 34\].
\[
  3\left( 0 \right) + 2y = 34 \\
  y = \dfrac{{34}}{2} \\
  y = 17 \;
 \]
Now, put the value of y as zero and find the value of x, from the equation \[3x + 2y = 34\].
$
  3x + 2\left( 0 \right) = 34 \\
  x = \dfrac{{34}}{3} \\
  x = 11.33 \;
 $
So, the y-intercept will be 17 and x-intercept will be 11.33.
By the above observation it can be observed that line \[3x + 2y = 34\], intersects x-axis at 11.33 and line \[3x + 2y = 34\], intersects y-axis at 17.

Note: This question is based on the concept of linear equation in two variables.
In two variables, an equation is said to be a linear equation if it is written in the form of \[ax + by + c = 0\], where a, b & c are real numbers and the coefficients of x and y are not equal to zero, i.e. a and b respectively.
The solution of linear equations in two variables, \[ax + by + c = 0\], is a special point in the graph, such that when an is multiplied by x-coordinate and b is multiplied by y-coordinate, the sum of these two values is equal to c.