Question

Let the cost of a pen and a pencil be \[{\rm{Rs}}.x\] and \[{\rm{Rs}}.y\] respectively. Anuj pays \[{\rm{Rs}}.34\] for 3 pens and 2 pencils. Write the given data in the form of a linear equation in two variables. Also represent it graphically.

Answer 1

Hint:
Here, we will frame a linear equation in two variables from the given conditions. We will substitute the different values of one variable in the equation to find another variable. Then we will use these values, which becomes the coordinates of the graph, to plot the equation graphically.

Complete step by step solution:
The cost of 3 pens can be found by multiplying the number of pens with the cost of a pen. So,
 Cost of 3 pens \[ = 3x\]
Now the cost of 2 pencils can be found by multiplying the number of pencils with the cost of a pencil. Therefore,
Cost of 2 pencils \[ = 2y\]
Thus the total cost paid can be found by adding the cost of 3 pens and cost of 2 pencils.
\[3x + 2y = 34\] ………………………………………………………………………………………………..\[\left( 1 \right)\]
By rewriting the equation, we get
\[ \Rightarrow 2y = 34 - 3x\]
\[ \Rightarrow y = \dfrac{{34 - 3x}}{2}\] ………………………………………………………………………………………………..\[\left( 2 \right)\]
By substituting \[x = 2\] in the equation \[\left( 2 \right)\], we get
\[y = \dfrac{{34 - 3\left( 2 \right)}}{2} = \dfrac{{34 - 6}}{2}\]
\[ \Rightarrow y = \dfrac{{28}}{2} = 14\]
By substituting \[x = 4\] in the equation \[\left( 2 \right)\], we get
\[y = \dfrac{{34 - 3\left( 4 \right)}}{2} = \dfrac{{34 - 12}}{2}\]
\[ \Rightarrow y = \dfrac{{22}}{2} = 11\]
By substituting \[x = 6\] in the equation \[\left( 2 \right)\], we get
\[y = \dfrac{{34 - 3\left( 6 \right)}}{2} = \dfrac{{34 - 18}}{2}\]
\[ \Rightarrow y = \dfrac{{16}}{2} = 8\]
By substituting \[x = 8\] in the equation \[\left( 2 \right)\], we get
\[y = \dfrac{{34 - 3\left( 8 \right)}}{2} = \dfrac{{34 - 24}}{2}\]
\[ \Rightarrow y = \dfrac{{10}}{2} = 5\]
By substituting \[x = 10\] in the equation \[\left( 2 \right)\], we get
\[y = \dfrac{{34 - 3\left( {10} \right)}}{2} = \dfrac{{34 - 30}}{2}\]
\[ \Rightarrow y = \dfrac{4}{2} = 2\]
So, the co-ordinates are \[\left( {2,14} \right)\],\[\left( {4,11} \right)\] , \[\left( {6,8} \right)\] ,\[\left( {8,5} \right)\] and \[\left( {10,2} \right)\]
Therefore, the co-ordinates are \[\left( {2,14} \right)\],\[\left( {4,11} \right)\] , \[\left( {6,8} \right)\] ,\[\left( {8,5} \right)\] and \[\left( {10,2} \right)\] .
Now, we plot the graph for the co-ordinates, we get

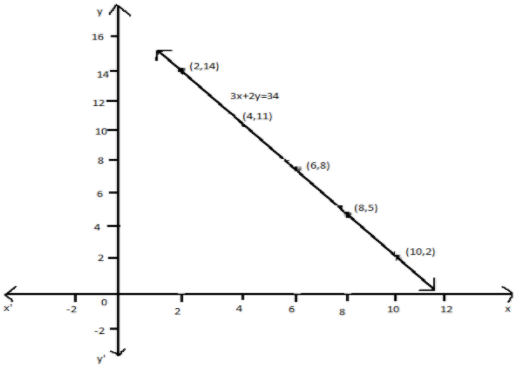
Note:
We have solved the linear equation in two variables by the method of substitution to find the solution set at different points. Thus the solution set becomes the coordinates of the point in the graph for the linear equation. Linear equation in two variables is an equation with the highest power of 1 in two variables. Thus the graph of a linear equation is always a straight line.