Question

Let ‘s’ denote the semiperimeter of a triangle ABC in which \[BC = a\] , \[CA = b\] , \[AB = c\] . If the circle touches the sides BC, CA, AB at D, E, F respectively, prove that \[BD = s - b\] .

Answer 1

Hint: We know that the semi perimeter of a triangle is given by \[s = \dfrac{{a + b + c}}{2}\] , where ‘a’ ‘b’ and ‘c’ are the length of sides of the triangle. We know the theorem that the length of tangents drawn from an external point to a circle are equal. Using this theorem we can solve the above theorem and we will draw a diagram using the given data in the above problem.

Complete step by step solution:
Let’s draw the diagram for the given data.
 \[BC = a\] , \[CA = b\] , \[AB = c\] .
Also the circle touches the sides BC, CA, AB at D, E, F respectively.

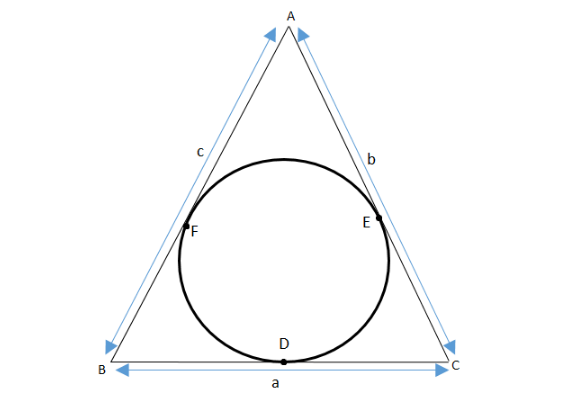
So the semi-perimeter is given according to the question is
 \[s = \dfrac{{a + b + c}}{2}\]
 \[ \Rightarrow 2s = a + b + c\] .
B is an external point and BD and BF are tangents and from an external point the tangents drawn to a circle are equal in length.
That is,
 \[BD = BF - - - (1)\] .
(The length of tangents drawn from an external point to a circle are equal.)
Similarly we have,
 \[AF = AE - - - (2)\] and \[CD = CE - - - (3)\] .
Also given ‘s’ is semi perimeter
 \[s = \dfrac{{AB + AC + BC}}{2}\]
 \[ \Rightarrow 2s = AB + AC + BC{\text{ }} - - - (4)\]
From the diagram we have,
 \[AB = AF + FB\]
 \[AC = AE + EC\]
 \[BC = BD + DC\]
Substituting these in equation (1) we have,
 \[ \Rightarrow 2s = AF + FB + AE + EC + BD + DC{\text{ }}\]
Now using equation (1), (2) and (3) we have,
 \[ \Rightarrow 2s = 2AE + 2EC + 2BD\]
 \[ \Rightarrow 2s = 2(AE + EC + BD)\]
 \[ \Rightarrow s = AE + EC + BD\]
But \[AE + EC = AC\] . (See in the above diagram)
 \[ \Rightarrow s = AC + BD\]
But we know that \[AC = b\]
 \[ \Rightarrow s = b + BD\]
 \[ \Rightarrow s - b = BD\]
Rearranging we have,
 \[ \Rightarrow BD = s - b\] .
Hence proved.

Note: We know that if we want perimeter we add all the side lengths of a given dimension. We know that the perimeter of a triangle is \[P = a + b + c\] , where ‘a’, ‘b’ and ‘c’ are the length of sides of the triangle. Since they asked for a semi we took half of the perimeter. To solve we need to remember particular theorems.