Question

Let \[{\rm P}\] be a point on the parabola, \[{x^2} = 4y\] If the distance of \[{\rm P}\] from the centre of the circle, \[{x^2} + {y^2} + 6x + 8 = 0\] is minimum, then the equation of the tangent to the parabola at \[{\rm P}\] , is?
A. \[x + 4y - 2 = 0\]
B. \[x + 2y = 0\]
C. \[x + y + 1 = 0\]
D. \[x - y + 3 = 0\]

Answer 1

Hint: In order to determine the equation of the tangent to the parabola at \[{\rm P}\] and the line drawn from the centre of the circle to point \[{\rm P}\] must be natural to the parabola \[{x^2} = 4y\] at the point \[{\rm P}\] in order for the distance between point \[{\rm P}\] \[\left( { - g, - f} \right)\] and the centre of the circle of the equation \[{x^2} + {y^2} + 6x + 8 = 0\] to be as small as possible. we use the tangent formula \[y - {y_1} = m(x - {x_1})\] with the point \[P({x_1},{y_1})\] to find the required answer.

Complete step-by-step answer:
We are given the \[{\rm P}\] be a point on the parabola, \[{x^2} = 4y\] , centre of the circle, \[{x^2} + {y^2} + 6x + 8 = 0\] is minimum.
We need to find out the equation of the tangent to the parabola at \[{\rm P}\]
Let the point \[{\rm P}\] on parabola be \[(2t,{t^2})\] and the centre \[\left( { - g, - f} \right)\] .Then the centre will be: \[\left( { - 3,{\text{ }}0} \right)\]
Now slope for line , \[m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\] from centre to point \[({x_1},{y_1}) = ( - 3,0)\] and \[({x_2},{y_2}) = (2t,{t^2})\]
 \[\
  m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}} = \dfrac{{{t^2} - 0}}{{2t + 3}} \\
  m = \dfrac{{{t^2}}}{{2t + 3}} \to (1) \;
\ \]
To find the slope of a line tangent to a parabola at a specific point, find the derivative of the parabola's equation,
 \[{x^2} = 4y\]
By differentiating the parabola equation with respect to x, we get
 \[\
  2xdx = 4dy \\
  \dfrac{{2x}}{4} = \dfrac{{dy}}{{dx}} \\
  \dfrac{{dy}}{{dx}} = \dfrac{x}{2} \;
\ \]
So, the slope of tangent to the parabola will be : \[m = \dfrac{x}{2} = t\]
Slope of normal is: \[ - \dfrac{1}{m} = - \dfrac{1}{t} \to (2)\]
Now, comparing the equation \[(1)\] and \[(2)\] , we can get
 \[\dfrac{{{t^2}}}{{2t + 3}} = - \dfrac{1}{t}\]
Expanding the equation on RHS, we can get
 \[\dfrac{{{t^2}}}{{2t + 3}} + \dfrac{1}{t} = 0\]
Take LCM on both side, we get
 \[\
  \dfrac{{t({t^2}) + 2t + 3}}{{t(2t + 3)}} = 0 \\
  {t^3} + 2t + 3 = 0 \;
\ \]
In this case we find that by substituting \[t\] with \[ - 1\] , it actually satisfies the equation, so \[ - 1\] is one of its roots. After that, divide the equation by \[t + 1\] (since \[ - 1\] is one of the roots) using long division. Now, we have \[{t^3} + 2t + 3 = (t + 1)({t^2} - t + 1)\]
With this we get a quadratic equation and by factoring it or using the quadratic formula, we can find the other 2 roots.
 \[(t + 1)({t^2} - t + 1) = 0\]
So, the real root will be \[(t + 1)\] : \[t = - 1\] and the coordinates of \[P(2t,{t^2})\] \[(2t,{t^2}) = (2( - 1),{( - 1)^2}) = ( - 2,1)\] .
Now, the slope of tangent to parabola at P will be: \[m = \dfrac{x}{2} = t = - 1\]
So the equation of tangent will be: \[y - {y_1} = m(x - {x_1})\] with the point \[({x_1},{y_1}) = ( - 2,1)\]
   \[\
  y - 1 = - 1(x - ( - 2)) \\
  y - 1 = - 1(x + 2) \\
  y - 1 + x + 2 = 0 \\
  x + y + 1 = 0 \;
\ \]
Finally, the point \[{\rm P}\] on the parabola, \[{x^2} = 4y\] If the distance of \[{\rm P}\] from the centre of the circle, \[{x^2} + {y^2} + 6x + 8 = 0\] is minimum, then the equation of the tangent to the parabola at \[{\rm P}\] , is \[x + y + 1 = 0\] .
Hence, the option( C ) \[x + y + 1 = 0\] is the correct answer.
So, the correct answer is “Option C”.

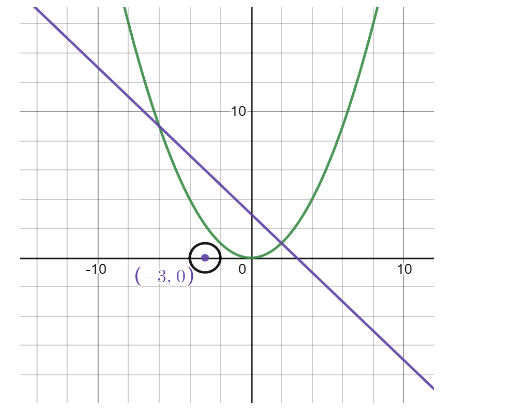
Note: First, we plot a graph is shown below
The green curve represent the parabola equation \[{x^2} = 4y\]
The blue line represent the tangent equation \[x + y + 1 = 0\]
The centre of the circle with the point \[\left( { - 3,{\text{ }}0} \right)\] of the equation \[{x^2} + {y^2} + 6x + 8 = 0\]
                     

We use the formula to find the slope of the line, \[m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\] and \[y - {y_1} = m(x - {x_1})\] is the formula for find out the equation of tangent.