
Let R be the set of real numbers and $f:R\to R$ be given by $f\left( x \right)=\sqrt{\left| x \right|}-\log \left( 1+\left| x \right| \right)$. We now make the following assertions: \[\]
I. There exists a real number $A$ such that $f\left( x \right)\le A$ for all $x$.\[\]
II. There exists a real number B such that $f\left( x \right)\ge B$ for all $x$.\[\]
A.I is true and II is false\[\]
B.I is false and II is true\[\]
C.I and II both are true\[\]
D.I and II both are false\[\]
Answer
565.2k+ views
Hint: We recall the definitions and critical points of a function and remember that maxima and minima of a function occur at the critical points. We use domain and range of the square root function and logarithmic function to conclude $\sqrt{\left| x \right|} > \log \left( 1+\left| x \right| \right)$ functions to conclude We try to find the critical points of the function to find $A$ and $B$. \[\]
Complete step-by-step solution:
We also know that the critical points of a function are the points where the first order derivative of the function is zero or the first derivative does not exist. Mathematically, $x=c$ is a critical point if $f'(c)=0$ or $f'(c)$ does not exist. The minima or maxima occur only at critical points. \[\]
We are given the following real valued $f:R\to R$ function in the question
\[f\left( x \right)=\sqrt{\left| x \right|}-\log \left( 1+\left| x \right| \right)\]
We see that we have a function which has two composite functions $\sqrt{\left| x \right|}$ and $\log \left( 1+\left| x \right| \right)$. We know that the first derivative of modulus function $\left| x \right|$ does not exist at $x=0$ and hence the first derivative of $f\left( x \right)$ will not exist at $x=0$. It makes $x=0$ a critical point of $f\left( x \right)$ and minima or maxima occur at $x=0$. We have
\[f\left( 0 \right)=\sqrt{\left| 0 \right|}-\log \left( 1+\left| 0 \right| \right)=0\]
We know from the graph of the logarithmic function that $\log x\ge 0$ for all $x\ge 1$ and $\log x < 0$ for all $x\le 1$. Then we have $\log \left| x \right|\ge 0$ for all $\left| x \right|\ge 1$ and $\log x < 0$ for all $x < 1$. We further have $\log \left( 1+\left| x \right| \right)\ge 0$ for all $\left| x \right|\ge 0$. We know that square function is defined from ${{R}^{+}}$ to ${{R}^{+}}$. Hence $\sqrt{\left| x \right|}\ge 0$ for all $x\ge 0$. The zero of $f\left( x \right)$that is $x=0$ is the point of intersection $\sqrt{\left| x \right|},\log \left( 1+\left| x \right| \right)$.\[\]
We see that as we move away from left and right side of $x=0$and we shall get $f\left( x \right) > 0$ since $\sqrt{\left| x \right|} > \log \left( 1+\left| x \right| \right)$ for all $x > 0$. So $f\left( x \right)$ will have a minimum at $x=0$. There exists a real number $B=0$ such that $f\left( x \right)\ge B$ for all$x$. The plot of the function is below which is symmetrical about positive $y-$axis.\[\]
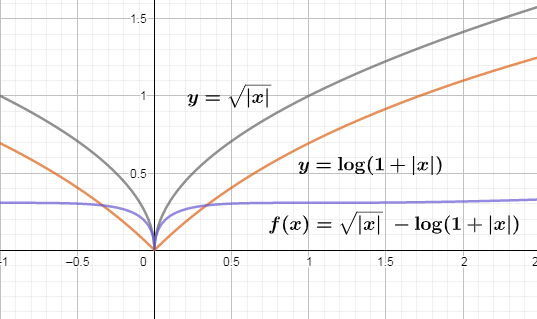
We see that $f\left( x \right)$ does not have a maxima for all $x\in R$.So there does not exist an $A$ such that $f\left( x \right)\le A$. So the statement (I) is false and statement ((II) is true and hence option B is correct. \[\]
Note: We note that there is only one critical point of the function. We can also use the first derivative test here but that will be difficult. We also note that if $f\left( x \right)$ is a real valued single function defined within some interval $I\subset D $ , it will have its local maximum value (called maxima) $x=a$ when $f\left( a \right) < f\left( x \right)$ for all $x\in I$ and local minimum value $x=a$ (called minima) when $f\left( a \right) > f\left( x \right)$ for all $x\in I$.
Complete step-by-step solution:
We also know that the critical points of a function are the points where the first order derivative of the function is zero or the first derivative does not exist. Mathematically, $x=c$ is a critical point if $f'(c)=0$ or $f'(c)$ does not exist. The minima or maxima occur only at critical points. \[\]
We are given the following real valued $f:R\to R$ function in the question
\[f\left( x \right)=\sqrt{\left| x \right|}-\log \left( 1+\left| x \right| \right)\]
We see that we have a function which has two composite functions $\sqrt{\left| x \right|}$ and $\log \left( 1+\left| x \right| \right)$. We know that the first derivative of modulus function $\left| x \right|$ does not exist at $x=0$ and hence the first derivative of $f\left( x \right)$ will not exist at $x=0$. It makes $x=0$ a critical point of $f\left( x \right)$ and minima or maxima occur at $x=0$. We have
\[f\left( 0 \right)=\sqrt{\left| 0 \right|}-\log \left( 1+\left| 0 \right| \right)=0\]
We know from the graph of the logarithmic function that $\log x\ge 0$ for all $x\ge 1$ and $\log x < 0$ for all $x\le 1$. Then we have $\log \left| x \right|\ge 0$ for all $\left| x \right|\ge 1$ and $\log x < 0$ for all $x < 1$. We further have $\log \left( 1+\left| x \right| \right)\ge 0$ for all $\left| x \right|\ge 0$. We know that square function is defined from ${{R}^{+}}$ to ${{R}^{+}}$. Hence $\sqrt{\left| x \right|}\ge 0$ for all $x\ge 0$. The zero of $f\left( x \right)$that is $x=0$ is the point of intersection $\sqrt{\left| x \right|},\log \left( 1+\left| x \right| \right)$.\[\]
We see that as we move away from left and right side of $x=0$and we shall get $f\left( x \right) > 0$ since $\sqrt{\left| x \right|} > \log \left( 1+\left| x \right| \right)$ for all $x > 0$. So $f\left( x \right)$ will have a minimum at $x=0$. There exists a real number $B=0$ such that $f\left( x \right)\ge B$ for all$x$. The plot of the function is below which is symmetrical about positive $y-$axis.\[\]
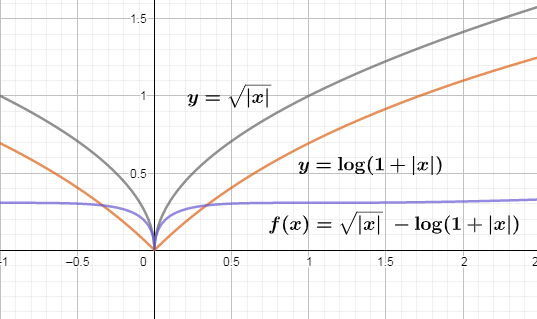
We see that $f\left( x \right)$ does not have a maxima for all $x\in R$.So there does not exist an $A$ such that $f\left( x \right)\le A$. So the statement (I) is false and statement ((II) is true and hence option B is correct. \[\]
Note: We note that there is only one critical point of the function. We can also use the first derivative test here but that will be difficult. We also note that if $f\left( x \right)$ is a real valued single function defined within some interval $I\subset D $ , it will have its local maximum value (called maxima) $x=a$ when $f\left( a \right) < f\left( x \right)$ for all $x\in I$ and local minimum value $x=a$ (called minima) when $f\left( a \right) > f\left( x \right)$ for all $x\in I$.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Why cannot DNA pass through cell membranes class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE




