Question

Let $R$ be the resultant of $P$ and $Q$ and if $\left( {\dfrac{P}{3}} \right) = \left( {\dfrac{Q}{7}} \right) = \left( {\dfrac{R}{5}} \right)$, then the angle between P and R is?
A) ${\cos ^{ - 1}}\left( {\dfrac{{11}}{{14}}} \right)$
B) ${\cos ^{ - 1}}\left( { - \dfrac{{11}}{{14}}} \right)$
C) $\dfrac{{2\pi }}{3}$
D) $\dfrac{{5\pi }}{6}$

Answer 1

Hint: Here, in the question, we are given that $R$ is the resultant of $P$ and $Q$ vector and we have to find the angle between the vector $P$ and the vector $R$. We know the formula to find the magnitude of resultant vector, which is $R = \sqrt {{P^2} + {Q^2} + 2PQ\cos \theta } $, here $P$, $Q$, $R$ are the magnitude of vectors and $\theta $ is the angle between vector $P$, $Q$. As we can see, in the given question the relation between three vectors is given so by using this we can find the value of $\theta $. There is an another relation, $\cos \phi {\text{}} = \dfrac{{P + Q\cos \theta }}{R}$ where $\phi $ is the angle between resultant vector $R$ and vector $P$ . So, from here we can find the value of the angle between $P$ and $R$.
Formula used:
$R = \sqrt {{P^2} + {Q^2} + 2PQ\cos \theta } $
On squaring both sides, we get
${R^2} = {P^2} + {Q^2} + 2PQ\cos \theta $
$\cos \phi {\text{}} = \dfrac{{P + Q\cos \theta }}{R}$

Complete answer:

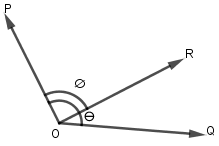
Given, $\dfrac{P}{3} = \dfrac{Q}{7} = \dfrac{R}{5}$
Let, $\lambda {\text{}} = \dfrac{P}{3} = \dfrac{Q}{7} = \dfrac{R}{5}$
Or we can write it as,
$ \Rightarrow \dfrac{P}{3} = \lambda ,\dfrac{Q}{7} = \lambda ,\dfrac{R}{5} = \lambda $
$ \Rightarrow P = 3\lambda ,Q = 7\lambda ,R = 5\lambda $
We know that, ${R^2} = {P^2} + {Q^2} + 2PQ\cos \theta $
Now, since we have values of $P$, $Q$ and $R$ we can substitute these values in the above written formula to get the value of $\cos \theta $.
$ \Rightarrow {\left( {5\lambda } \right)^2} = {\left( {3\lambda } \right)^2} + {\left( {7\lambda } \right)^2} + 2\left( {3\lambda } \right)\left( {7\lambda } \right)\cos \theta $
On simplifying, we get
$ \Rightarrow 25{\lambda ^2} = 9{\lambda ^2} + 49{\lambda ^2} + 42{\lambda ^2}\cos \theta $
Shift $9{\lambda ^2}$ and $49{\lambda ^2}$ to LHS,
$ \Rightarrow 25{\lambda ^2} - 9{\lambda ^2} - 49{\lambda ^2} = 42{\lambda ^2}\cos \theta $
$ \Rightarrow {\text{}} - 33{\lambda ^2} = 42{\lambda ^2}\cos \theta $
It can also be written as,
$ \Rightarrow 42{\lambda ^2}\cos \theta {\text{}} = {\text{}} - 33{\lambda ^2}$
\[ \Rightarrow \cos \theta {\text{}} = \dfrac{{ - 33{\lambda ^2}}}{{42{\lambda ^2}}}\]
After cancelling out ${\lambda ^2}$ and division, we get
\[ \Rightarrow \cos \theta {\text{}} = \dfrac{{ - 11}}{{14}}\]
As we know that $\cos \phi {\text{}} = \dfrac{{P + Q\cos \theta }}{R}$.
Now, we will substitute the values of $P$, $Q$, $R$ and $\cos \theta $ in the above written formula.
$ \Rightarrow \cos \phi {\text{}} = \dfrac{{3\lambda {\text{}} + 7\lambda \left( {\dfrac{{ - 11}}{{14}}} \right)}}{{5\lambda }}$
Take $\lambda $ as a common factor
$ \Rightarrow \cos \phi {\text{}} = \dfrac{{\lambda \left( {3 + 7\left( {\dfrac{{ - 11}}{{14}}} \right)} \right)}}{{5\lambda }}$
On cancelling out $\lambda $, we get
$ \Rightarrow \cos \phi {\text{}} = \dfrac{{\left( {3 + 7\left( {\dfrac{{ - 11}}{{14}}} \right)} \right)}}{5} = \dfrac{{3 + \left( {\dfrac{{ - 11}}{2}} \right)}}{5}$
\[ \Rightarrow \cos \phi {\text{}} = \dfrac{{3 - \dfrac{{11}}{2}}}{5}\]
Solve the numerator by taking LCM
$ \Rightarrow \cos \phi {\text{}} = \dfrac{{\dfrac{{6 - 11}}{2}}}{5}$
\[ \Rightarrow \cos \phi {\text{}} = \dfrac{{\dfrac{{ - 5}}{2}}}{5}\]
It can also be written as,
\[ \Rightarrow \cos \phi {\text{}} = \dfrac{{ - 5}}{2} \times \dfrac{1}{5}\]
\[ \Rightarrow \cos \phi {\text{}} = \dfrac{{ - 1}}{2}\]
On shifting $\cos $ to RHS, we get
$ \Rightarrow \phi {\text{}} = {\cos ^{ - 1}}\left( {\dfrac{{ - 1}}{2}} \right)$
We know that, ${\cos ^{ - 1}}\left( { - x} \right) = \pi {\text{}} - {\cos ^{ - 1}}x,x \in \left[ { - 1,1} \right]$. Therefore, we get
$ \Rightarrow \phi {\text{}} = \pi {\text{}} - {\cos ^{ - 1}}\left( {\dfrac{1}{2}} \right)$
We know that $\cos \dfrac{\pi }{3} = \dfrac{1}{2}$. So, on replacing, we get
$ \Rightarrow \phi {\text{}} = \pi {\text{}} - {\cos ^{ - 1}}\left( {\cos \dfrac{\pi }{3}} \right)$
Also, we know ${\cos ^{ - 1}}\left( {\cos \theta } \right) = \theta $. Therefore, we get
$ \Rightarrow \phi {\text{}} = \pi {\text{}} - \dfrac{\pi }{3}$
$ \Rightarrow \phi {\text{}} = \dfrac{{2\pi }}{3}$
Thus, the angle between $P$ and $R$ is $\dfrac{{2\pi }}{3}$.
Therefore, the correct option is C.

Note:
Here, in the given question we have found the value of angle between $P$ and $R$ using the formula $\cos \phi {\text{}} = \dfrac{{P + Q\cos \theta }}{R}$. If the question was about finding the value of the angle between $Q$ and $R$ we will not apply this formula. We will use $\cos \phi {\text{}} = \dfrac{{Q + P\cos \theta }}{R}$. To solve these type of questions we should know all the required values of standard angles say,${0^\circ }$, ${30^\circ }$, ${60^\circ }$, ${90^\circ }$, ${180^\circ }$, ${270^\circ }$, ${360^\circ }$ respectively for each trigonometric term such as $\sin $, $\cos $, $\tan $, $\cot $, $\sec $, $\cos ec$, etc.