Question

Let ‘PA’ and ‘PB’ are the two tangents drawn from the point P(0,-2) to the circle \[{{x}^{2}}+{{y}^{2}}+2x-4y=0\]. Then the angle between PA and PB is

(a) \[{{\tan }^{-1}}\left( \dfrac{4\sqrt{15}}{7} \right)\]
(b) \[{{\tan }^{-1}}\left( \dfrac{8\sqrt{15}}{7} \right)\]
(c) \[{{\tan }^{-1}}\left( \dfrac{16\sqrt{15}}{7} \right)\]
(d) \[{{\tan }^{-1}}\left( \dfrac{6\sqrt{15}}{7} \right)\]

Answer 1

Hint:For this type of geometry question you need to draw the figure that represents given data as follows.

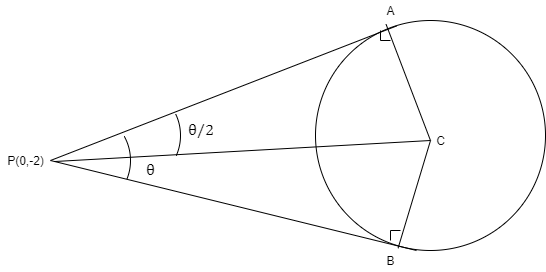
Complete step by step answer:
Here we have two triangles and we know that these two are congruent so we can take \[\angle APC=\dfrac{1}{2}\left( \angle APB \right)\] and find value of \[\tan \left( \dfrac{\theta }{2} \right)\] and then using trigonometric formula given below and calculate for \[\tan \theta \].
 \[\tan \theta =\dfrac{2\tan \left( \dfrac{\theta }{2} \right)}{1-{{\tan }^{2}}\left( \dfrac{\theta }{2} \right)}\]
From the properties of tangents we know that \[\Delta ACP\]is congruent to \[\Delta BCP\]
So, let us assume that \[\angle APB\] = \[\theta \]then \[\angle ACP\]= \[\dfrac{\theta }{2}\]
From \[\Delta ACP\] we can write
\[\tan \left( \dfrac{\theta }{2} \right)=\dfrac{AC}{AP}\] ……………..equation (i)
Now, let us find AC (radius of circle) and CP (distance between two points) to get AP.
Taking the given equation of circle
\[{{x}^{2}}+{{y}^{2}}+2x-4y=0\] …………………..equation (ii)
Converting this equation of circle into general form that is
\[{{(x-{{x}_{1}})}^{2}}+{{(y-{{y}_{1}})}^{2}}={{r}^{2}}\]
We will get radius ‘r’ and co-ordinates of centre of the circle as (\[{{x}_{1}},{{y}_{1}}\])
Now, adding 5 on both sides of equation (ii) we get
\[\begin{align}
  & \Rightarrow {{x}^{2}}+{{y}^{2}}+2x-4y+5=5 \\
 & \Rightarrow ({{x}^{2}}+2x+1)+({{y}^{2}}-4y+4)=5 \\
 & \Rightarrow \left[ {{(x)}^{2}}+2(x)(1)+{{(1)}^{2}} \right]+\left[ {{(y)}^{2}}+2(y)(-2)+{{(-2)}^{2}} \right]=5 \\
\end{align}\]
Now using the formula \[{{a}^{2}}+2ab+{{b}^{2}}={{(a+b)}^{2}}\] we get
\[\Rightarrow {{(x+1)}^{2}}+{{(y-2)}^{2}}={{(\sqrt{5})}^{2}}\]
Here the radius of given circle is \[\sqrt{5}\]and co-ordinates of centre is (-1,2) that is
AC = \[\sqrt{5}\] and co-ordinates of centre C = (-1,2)
For finding PC we use distance between two point formula that is
\[PC=\sqrt{{{({{x}_{1}}-{{x}_{2}})}^{2}}+{{({{y}_{1}}-{{y}_{2}})}^{2}}}\], where \[({{x}_{1}},{{y}_{1}})\text{ and (}{{\text{x}}_{2}},{{y}_{2}})\] are co-ordinates of points P and C respectively
Substituting values of \[({{x}_{1}},{{y}_{1}})\text{ and (}{{\text{x}}_{2}},{{y}_{2}})\] with corresponding values of (0,-2) and (-1,2) we get
\[\begin{align}
  & \Rightarrow PC=\sqrt{{{(0-(-1))}^{2}}+{{(2-(-2))}^{2}}} \\
 & \Rightarrow PC=\sqrt{1+16} \\
 & \Rightarrow PC=\sqrt{17} \\
\end{align}\]
Considering \[\Delta ACP\] and applying Pythagoras theorem (square of hypotenuse is equal to sum of squares of other two sides)
\[P{{C}^{2}}=A{{C}^{2}}+A{{P}^{2}}\]
Substituting values of PC and AC we get
\[\begin{align}
  & \Rightarrow {{(\sqrt{17})}^{2}}={{(\sqrt{5})}^{2}}+A{{P}^{2}} \\
 & \Rightarrow A{{P}^{2}}=17-5 \\
 & \Rightarrow AP=\sqrt{12} \\
\end{align}\]
Now, from equation (i) substituting the required values we get
\[\tan \left( \dfrac{\theta }{2} \right)=\dfrac{\sqrt{5}}{\sqrt{12}}\]
Now, for finding the angle we use half-angle formula that is
\[\tan \theta =\dfrac{2\tan \left( \dfrac{\theta }{2} \right)}{1-{{\tan }^{2}}\left( \dfrac{\theta }{2} \right)}\]
Substituting \[\tan \left( \dfrac{\theta }{2} \right)=\dfrac{\sqrt{5}}{\sqrt{12}}\] in above equation we get
\[\begin{align}
  & \Rightarrow \tan \theta =\dfrac{2\left( \dfrac{\sqrt{5}}{\sqrt{12}} \right)}{1-{{\left( \sqrt{\dfrac{5}{12}} \right)}^{2}}} \\
 & \Rightarrow \tan \theta =\dfrac{2\left( \dfrac{\sqrt{5}}{2\sqrt{3}} \right)}{1-\dfrac{5}{12}} \\
\end{align}\]
Evaluating the value in denominator and taking reciprocal of denominator we get
\[\Rightarrow \tan \theta =\dfrac{\sqrt{5}}{\sqrt{3}}.\dfrac{12}{7}\]
By writing 12 as \[\left( 4\sqrt{3} \right)\left( \sqrt{3} \right)\] and cancelling \[\sqrt{3}\] in numerator and denominator we get
\[\begin{align}
  & \Rightarrow \tan \theta =\dfrac{\sqrt{5}.4.\sqrt{3}}{7} \\
 & \Rightarrow \tan \theta =\dfrac{4\sqrt{15}}{7} \\
\end{align}\]
Finally taking inverse of tangent function we get
\[\Rightarrow \theta ={{\tan }^{-1}}\left( \dfrac{4\sqrt{15}}{7} \right)\]

So, option (a) is the correct answer
Note:
 The main mistake can only be done in the calculation part. Considering all the parameters required correctly plays important role in solving this problem. We need to find only the required parameters to reduce problem-solving time and place that is we need values of sides of \[\Delta ACP\] there is no need to find the value of AB or the other angle of \[\Delta ACP\] which may only make your solution taking more time.