Question

Let P be the point (3,0) and Q be a moving point (0,3t). Let PQ be trisected at R so that R is nearer to Q. RN is drawn perpendicular to PQ meeting the x-axis at N. The locus of the midpoint of RN is
(a) ${{\left( x+3 \right)}^{2}}-3y=0$
(b) \[{{\left( y+3 \right)}^{2}}-3x=0\]
(c) \[{{x}^{2}}-y=1\]
(d) \[{{y}^{2}}-x=1\]

Answer 1

Hint: Point of trisection means a point which exactly divides a line segment into three equal parts. Here, point R divides a line segment PQ into 3 parts but point R is closer to Q hence dividing the line segment PQ in a ratio of 2:1 internally. First we have to find out the point of division and then the locus of midpoint by applying the midpoint formula.

Complete step-by-step answer:

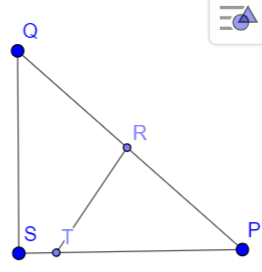
 The point P which divides the line segment joining the points A \[\left( {{x}_{1,}}{{y}_{1}} \right)\], B \[\left( {{x}_{2}},{{y}_{2}} \right)\]in the ratio m:n internally is given by
P = \[\left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)\]
P(3,0) and Q(0,3t) are given. Now we have to find R which divides P and Q internally in the ratio 2:1.
R= \[\left( \dfrac{2(0)+1(-3)}{2+1},\dfrac{2(3t)+1(0)}{2+1} \right)\]
R = (-1,2t)
Now consider the point N as (x,0) because it is lying on the x axis and the line RN is perpendicular to PQ.
Slope of PQ $\times $slope of RN = -1
Because the product of slopes of two perpendicular lines is -1.
\[\dfrac{3t-0}{0-(-3)}\times \dfrac{2t-0}{-1-x}=-1\]
$\begin{align}
  & 2{{t}^{2}}=x+1 \\
 & x=2{{t}^{2}}-1 \\
\end{align}$
$\begin{align}
  & 2{{t}^{2}}=x+1 \\
 & x=2{{t}^{2}}-1 \\
\end{align}$
 The point N is \[\left( 2{{t}^{2}}-1,0 \right)\]

 The locus of midpoint of RN is
Formula for midpoint is: \[\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)\]
The midpoint of RN is \[\left( \dfrac{2{{t}^{2}}-1+\left( -1 \right)}{2},\dfrac{2t+0}{2} \right)\]
(x,y) = \[\left( {{t}^{2}}-1,t \right)\]
Therefore y=t, x= \[{{t}^{2}}-1\]
\[\therefore \] \[x={{y}^{2}}-1\]
Therefore the option is d.

So, the correct answer is “Option d”.

Note: When two lines are perpendicular to each other the product of their slopes is equal to -1. R can divide P and Q in the ratio 1:2 and 2:1 internally. Here we have to take 2:1 because it was given that R is closer to Q.