Question

Let $\overline{PQ}$ be perpendicular to the line segment $\overline{XY}$. Let $\overline{PQ}$ and $\overline{XY}$ intersect at a point A. What is the measure of angle $\angle PAY$ ?

Answer 1

Hint: Here, we have been given with two-line segments which intersect at a point A. These line segments are namely $\overline{PQ}$ and $\overline{XY}$ . We shall make use of the fact that the line segment $\overline{PQ}$ is perpendicular to the line segment $\overline{XY}$ at the time of intersection to calculate the measure of angle $\angle PAY$.


Complete step by step solution:
Let us first of all draw a neat and clean diagram with proper labels to understand our problem better. This can be done as follows:

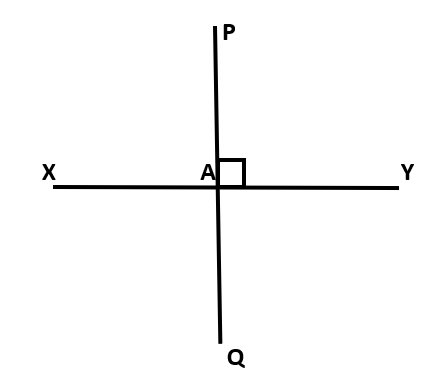
Here, we can clearly see that the line segment $\overline{PQ}$ is perpendicular to the line segment $\overline{XY}$. This implies that the line segments $\overline{PQ}$ and $\overline{XY}$ are at right angles to each other. This means that all the angles made by these two lines with each other is equal to ${{90}^{\circ }}$.
Therefore, the measure of $\angle PAY$ is also equal to ${{90}^{\circ }}$.

We can convert this angle in degrees into its standard measurement, that is, measurement in radians. This can be done as follows:
We know that, ${{360}^{\circ }}$ is equal to $2\pi $radians.
Therefore, ${{90}^{\circ }}$ will be equal to:
$\begin{align}
  & \Rightarrow {{90}^{\circ }}=\dfrac{2\pi }{{{360}^{\circ }}}\times {{90}^{\circ }} \\
 & \Rightarrow {{90}^{\circ }}=\dfrac{2\pi }{4} \\
 & \therefore {{90}^{\circ }}=\dfrac{\pi }{2}radians \\
\end{align}$
Therefore, the measure of $\angle PAY$ in radians comes out to be $\dfrac{\pi }{2}radians$
Hence, the measure of angle $\angle PAY$ is equal to ${{90}^{\circ }}$ or $\dfrac{\pi }{2}$radians.

Note: We should always know the meaning of different statements used in angle measurement. Some examples are: if two lines are perpendicular or at right angles, then the angle subtended between them is equal to ${{90}^{\circ }}$. If the two lines are parallel, the angle subtended is ${{0}^{\circ }}$ and if they are anti-parallel, then the angle subtended is equal to ${{180}^{\circ }}$. These statements should be remembered thoroughly as they are used very often.