Question

Let $\overline{a},\overline{b},\overline{c},\overline{d}$ be position vectors of four points A, B, C and D lying in a plane. If $\left( \overline{a}-\overline{d} \right).\left( \overline{b}-\overline{c} \right)=0=\left( \overline{b}-\overline{d} \right).\left( \overline{c}-\overline{a} \right)$ , then $\Delta ABC$ has D as:
(a) in-centre
(b) circum-centre
(c) ortho-centre
(d) centroid

Answer 1

Hint: We know that if the dot product of two vectors is 0 this means that the two vectors are perpendicular to each other. And it is given that if ABC is a triangle then we are asked about the point D. As you can see that point D $\left( or\text{ }\overline{\text{d}} \right)$ has occurred in both the dot products given in the above problem so the point D will lie inside the triangle ABC.

Complete step by step answer:
In the above problem, it is given that from the three position vectors with points A, B and C, a triangle has been constructed and the point D lies inside the circle.

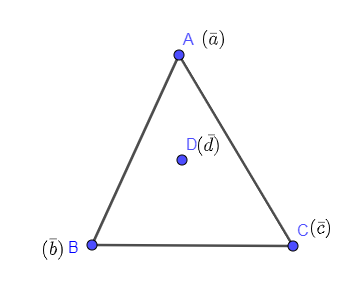
Also, there is a relation between the vectors $\overline{a},\overline{b},\overline{c},\overline{d}$ which we are shown below:
$\left( \overline{a}-\overline{d} \right).\left( \overline{b}-\overline{c} \right)=0=\left( \overline{b}-\overline{d} \right).\left( \overline{c}-\overline{a} \right)$
We know that when the two vectors are perpendicular to each other then their dot product is 0 so the vectors $\left( \overline{a}-\overline{d} \right)\And \left( \overline{b}-\overline{c} \right)$ are perpendicular to each other. Also the vectors $\left( \overline{b}-\overline{d} \right)\And \left( \overline{c}-\overline{a} \right)$ are perpendicular to each other.
Now, we can write $\left( \overline{a}-\overline{d} \right)$ as AD and $\left( \overline{b}-\overline{c} \right)$ as BC and $\left( \overline{b}-\overline{d} \right)$ as BD and $\left( \overline{c}-\overline{a} \right)$ as CA. Drawing these vectors in the given triangle. Also, make sure that the vectors whose dot product is 0 are perpendicular to each other.

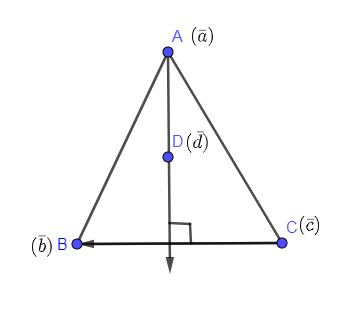
In the above problem we have drawn $\left( \overline{a}-\overline{d} \right)\And \left( \overline{b}-\overline{c} \right)$.
Now, drawing $\left( \overline{b}-\overline{d} \right)\And \left( \overline{c}-\overline{a} \right)$ we get,

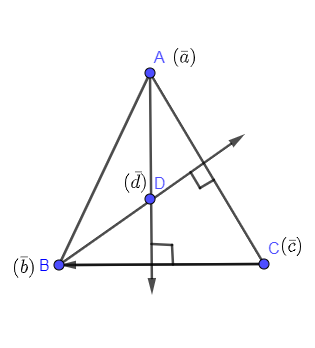
We know that orthocenter is the point in the triangle which is the intersection of all the altitudes passing through three vertices of the triangle. This means point D is the orthocenter of the triangle.
So, the correct answer is “Option c”.

Note: In the above problem, we have learnt that when the dot product of two vectors is 0 then those two vectors are perpendicular to each other. Also, we have learnt that intersection of altitudes of the three vertices of a triangle is the orthocenter.