Question

Let $h(x) = {e^{ - x}} + kx,$ where $k$ is any constant. For what value(s) of $k$ does $h$ have, no critical points?
A. $k > 0$
B. $k = 0$
C. $k < 0$
D. $k \leqslant 0$
E. $k > 0$

Answer 1

Hint: At critical points $f'(x) = 0$
Differentiate the equation given in the question and equate it to zero to solve the question.

Complete Step by Step Solution:
We have, $h(x) = {e^{ - x}} + kx$,$k$is constant
At critical point, $\dfrac{d}{{dx}}[h(x)] = 0$
$ \Rightarrow \dfrac{d}{{dx}}({e^{ - x}} + kx) = 0$
$\because \dfrac{d}{{dx}}{e^{ax}} = a{e^{ax}}$ and $\dfrac{d}{{dx}}{x^n} = n{x^{n - 1}}$
We get
$\dfrac{d}{{dx}}({e^{ - x}} + kx) = \dfrac{d}{{dx}}({e^{ - x}}) + \dfrac{d}{{dx}}kx$
$ = - {e^{ - x}} + k(1)$ (Since differentiation is distinctive over addition)
$ \Rightarrow - {e^{ - x}} + k = 0$
$ \Rightarrow k = {e^{ - x}}.$
From the graph of ${e^{ - x}}$, we can observe that ${e^{ - x}} > 0$ for all the values of $x.$

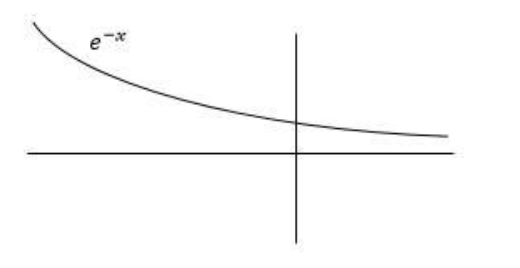
$ \Rightarrow k = {e^{ - x}} > 0$
$ \Rightarrow k > 0$
Therefore, at $k > 0$, we will get critical points.
Thus, for $k \leqslant 0$, we will not get critical points.

Therefore, the answer is D. $k \leqslant 0$

Note:
To solve such a type of question you need to know the range of basic functions like trigonometric functions, logarithmic function and exponential function. Also, you need to understand the concept of inequality knowing the graphs of basic function will always help you.