Question

Let $f\left( x \right)=\dfrac{\sin \pi x}{{{x}^{2}}},x>0.$ Let ${{x}_{1}}<{{x}_{2}}<{{x}_{3}}.....<{{x}_{n}}<.....$be all the points of local maximum of f(x) and ${{y}_{1}}<{{y}_{2}}<{{y}_{3}}.....<{{y}_{n}}<.....$be all the points of local minimum of f(x). Then which of the following is/are correct:
(a) $\left| {{x}_{n}}-{{y}_{n}} \right|>1$for every n
(b) ${{x}_{1}}<{{y}_{1}}$
(c) ${{x}_{n+1}}-{{x}_{n}}>2$for every n
(d) ${{x}_{n}}\in \left( 2n,2n+\dfrac{1}{2} \right)$ for every n

Answer 1

Hint: First, before proceeding for this, we must find the first derivate of the given function to get the maximum and minimum values of the function. Then, by taking $2\cos \pi x$common from the numerator and by using the identity of trigonometry $\tan x=\dfrac{\sin x}{\cos x}$. Then, by using the graphs of the $\cos \pi x$ and $\tan \pi x$, we get all the correct options.

Complete step by step answer:
In this question, we are supposed to find the correct option/s when $f\left( x \right)=\dfrac{\sin \pi x}{{{x}^{2}}},x>0.$ and also ${{x}_{1}}<{{x}_{2}}<{{x}_{3}}.....<{{x}_{n}}<.....$be all the points of local maximum of f(x) and ${{y}_{1}}<{{y}_{2}}<{{y}_{3}}.....<{{y}_{n}}<.....$be all the points of local minimum of f(x).
So, before proceeding for this, we must find the first derivate of the given function to get the maximum and minimum values of the function as:
$\begin{align}
  & {f}'\left( x \right)=\dfrac{{{x}^{2}}\dfrac{d}{dx}\sin \pi x-\sin \pi x\dfrac{d}{dx}{{x}^{2}}}{{{x}^{4}}} \\
 & \Rightarrow {f}'\left( x \right)=\dfrac{{{x}^{2}}\pi \cos \pi x-2x\sin \pi x}{{{x}^{4}}} \\
 & \Rightarrow {f}'\left( x \right)=\dfrac{x\pi \cos \pi x-2\sin \pi x}{{{x}^{3}}} \\
\end{align}$
Now, by taking $2\cos \pi x$common from the numerator and by using the identity of trigonometry $\tan x=\dfrac{\sin x}{\cos x}$, we get:
${f}'\left( x \right)=\dfrac{2\cos \pi x\left( \dfrac{\pi x}{2}-\tan \pi x \right)}{{{x}^{3}}}$
Now, by using the graphs of the $\cos \pi x$ and $\tan \pi x$as:

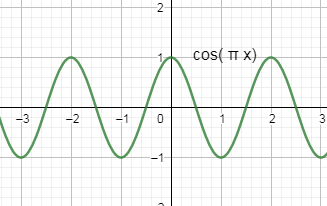
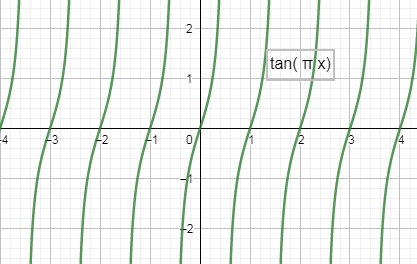
So, we can see clearly from both the graphs that $\cos \pi x$ and $\tan \pi x$ both are positive in the interval of $\left( 2n,2n+\dfrac{1}{2} \right)$.
So, option (d) is correct.
Moreover, from the range we can also see that ${{x}_{n+1}}-{{x}_{n}}>2$ which proves option (c) to be correct.
Also, we can se that the graph of the two when subtracted always gives the value larger than 1 irrespective of sign as it is a modulus function which proves $\left| {{x}_{n}}-{{y}_{n}} \right|>1$.
Hence, options (a), (c) and (d) are correct.

Note:
Now, to solve these type of the questions we need to know some of the basic formulas for the differentiation to get the answer correctly. So, the formula for the differentiation is as:
$\begin{align}
  & \dfrac{d}{dx}\left( \dfrac{u}{v} \right)=\dfrac{v\dfrac{d}{dx}u-u\dfrac{d}{dx}v}{{{v}^{2}}} \\
 & \dfrac{d}{dx}\operatorname{sina}x=a\operatorname{cosa}x \\
 & \dfrac{d}{dx}{{x}^{n}}=n{{x}^{n-1}} \\
\end{align}$