Question

Let \[f:\left[ { - \dfrac{1}{2},2} \right] \to R\] and $g:\left[ { - \dfrac{1}{2},2} \right] \to R$ be function defined by $f(x) = \left[ {{x^{^2}} - 3} \right]$ and $g(x) = \left| x \right|f(x) + \left| {4x - 7} \right|f(x),$ where $\left[ {} \right]$denotes the greatest integer less than or equal to $y \in R$. Then
(A) $f$ is discontinuous at three point in \[\left[ { - \dfrac{1}{2},2} \right]\]
(B) $f$ is discontinuous at four point in \[\left[ { - \dfrac{1}{2},2} \right]\]
(C) $g$ is NOT differentiable exactly at four point in \[\left( { - \dfrac{1}{2},2} \right)\]
(D) $g$ is NOT differentiable exactly at five point in \[\left( { - \dfrac{1}{2},2} \right)\]

Answer 1

Hint: First we find point of discontinuity of $f(x) = \left[ {{x^{^2}} - 3} \right]$ by making graph. As we see that given function is a greatest integer function so it define only at integer point.
Next from the point of discontinuity of $f(x)$ we define the function $g(x) = \left| x \right|f(x) + \left| {4x - 7} \right|f(x),$
And find a point where it is not differentiable.

Complete step by step answer:
Given $f(x) = \left[ {{x^{^2}} - 3} \right]$ is a greatest integer function and define in $ - \dfrac{1}{2} \leqslant x \leqslant 2$
Now we find ${x^2} - 3$ is define where
from the value of $x$
we say that $0 \leqslant {x^2} \leqslant 4$
now subtract 3 from above given equation
$ \Rightarrow - 3 \leqslant {x^2} - 3 \leqslant 1$
Now take a greatest integer
$ \Rightarrow - 3 \leqslant [{x^2} - 3] \leqslant 1$
From this we can say $f(x)$ take value from $\left[ { - 3,1} \right]$ only at integer value.
\[f(x) = \{ - 3,, - 2, - 1,0,1\} \]
Now
1.$f(x) = - 3$
Then $\left[ {{x^2} - 3} \right] = - 3$
So $ - 3 \leqslant {x^2} - 3 \leqslant - 2$
$ \Rightarrow 0 \leqslant {x^2} \leqslant 1$
From here $ - 1 \leqslant x \leqslant 1$
2. $f(x) = - 2$
Then $\left[ {{x^2} - 3} \right] = - 2$
So $ - 2 \leqslant {x^2} - 3 \leqslant - 1$
$ \Rightarrow 1 \leqslant {x^2} \leqslant 2$
Now we take square root to find $x$
From here $1 \leqslant x \leqslant \sqrt 2 $
3. $f(x) = - 1$
Then $\left[ {{x^2} - 3} \right] = - 1$
So $ - 1 \leqslant {x^2} - 3 \leqslant 0$
$ \Rightarrow 2 \leqslant {x^2} \leqslant 3$
Now we take square root to find $x$
From here $\sqrt 2 \leqslant x \leqslant \sqrt 3 $
4. $f(x) = 0$
Then $\left[ {{x^2} - 3} \right] = 0$
So $0 \leqslant {x^2} - 3 \leqslant 1$
$ \Rightarrow 3 \leqslant {x^2} \leqslant 4$
Now we take square root to find $x$
From here $\sqrt 3 \leqslant x \leqslant 2$
5$f(x) = 1$
Then $\left[ {{x^2} - 3} \right] = 1$
So $1 \leqslant {x^2} - 3 \leqslant 2$
$ \Rightarrow 4 \leqslant {x^2} \leqslant 5$

Now we take the square root to find $x$
From here $2 \leqslant x \leqslant \sqrt 5 $ but we know that function can not take value more than 2
So $x = 2$

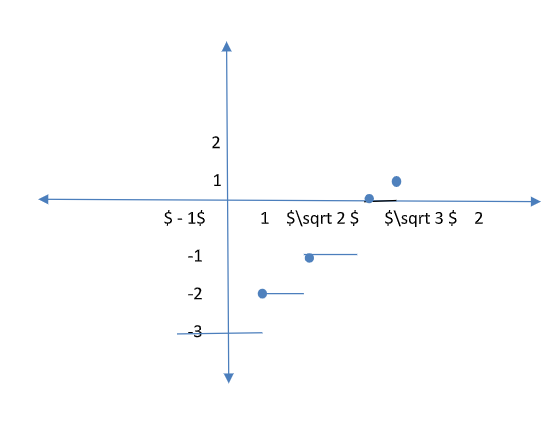
So from this, we can say it is discontinuous at 4 points.
Point of discontinuity $\left\{ {1,\sqrt 2 ,\sqrt 3 ,2,} \right\}$
So option B is the correct answer.
Now for function $g(x) = \left| x \right|f(x) + \left| {4x - 7} \right|f(x),$
By putting value of $f(x)$
So first when $ - 1 \leqslant x < 1$ here $f(x) = - 3$
So $g(x) = - 3\left| x \right| - 3\left| {4x - 7} \right|$
When $ - 1 \leqslant x < 0$ then $g(x) = 3x + 3\left( {4x - 7} \right)$
$g(x) = 15x - 21$
And when $0 \leqslant x < 1$
In this $\left| {4x - 7} \right|$ open with negative sign
So $g(x) = - 3x + 3\left( {4x - 7} \right)$
$g(x) = 9x - 21$

2. when $1 \leqslant x < \sqrt 2 $; $f(x) = - 2$
So $g(x) = - 2\left| x \right| - 2\left| {4x - 7} \right|$
In this $\left| {4x - 7} \right|$ open with negative sign
so $g(x) = - 2x + 2\left( {4x - 7} \right)$
$g(x) = 6x - 14$

3. when $\sqrt 2 \leqslant x < \sqrt 3 $; $f(x) = - 1$
So $g(x) = - \left| x \right| - \left| {4x + 7} \right|$
In this $\left| {4x - 7} \right|$ open with negative sign
so $g(x) = 3x - 7$

4. When $\sqrt 3 \leqslant x < 2$; $f(x) = 0$
So $g(x) = 0$.

5. when $x = 2;f(x) = 1$
So $g(x) = \left| x \right| + \left| {4x - 7} \right|$
$g(x) = 5x - 7$
Now we have to find differentiability of \[g(x)\]
(i) At $x = 0$
Right hand derivative $g'(a + ) = \mathop {\lim }\limits_{h \to 0} \dfrac{{f(a + h) - f(a)}}{h}$
So $g'(0 + ) = \mathop {\lim }\limits_{h \to 0} \dfrac{{f(0 + h) - f(0)}}{h}$
$g'(0 + ) = \mathop {\lim }\limits_{h \to 0} \dfrac{{9h - 21 + 21}}{h}$
So $g'(0 + ) = \mathop {\lim }\limits_{h \to 0} \dfrac{{9h}}{h} = 9$.
So right hand derivative = 9
Now left hand derivative
$g'(a - ) = \mathop {\lim }\limits_{h \to 0} \dfrac{{f(a - h) - f(a)}}{{ - h}}$
So $g'(0 - ) = \mathop {\lim }\limits_{h \to 0} \dfrac{{f(0 - h) - f(0)}}{{ - h}}$
$g'(0 - ) = \mathop {\lim }\limits_{h \to 0} \dfrac{{15h - 21 + 21}}{{ - h}}$
$g'(0 - ) = \mathop {\lim }\limits_{h \to 0} \dfrac{{15h}}{{ - h}} = - 15$
So left hand limit is not equal to right hand limit so function $g(x)$ is not deprivable at $x = 0$
(ii). At $x = 1$
Left hand derivative
$g'(1 - ) = \mathop {\lim }\limits_{h \to 0} \dfrac{{f(1 - h) - f(1)}}{{ - h}}$
$g'(1 - ) = \mathop {\lim }\limits_{h \to 0} \dfrac{{9\left( {1 - h} \right) - 21 - 6 + 14}}{{ - h}}$
$g'(1 - ) = \mathop {\lim }\limits_{h \to 0} \dfrac{{ - 9h - 4}}{{ - h}}$
By using L’HOSPITAL RULE
$g'(1 - ) = \mathop {\lim }\limits_{h \to 0} \dfrac{{ - 9}}{{ - 1}} = 9$
And right hand limit.
$g'(1 + ) = \mathop {\lim }\limits_{h \to 0} \dfrac{{f(1 + h) - f(1)}}{h} = \mathop {\lim }\limits_{h \to o} \dfrac{{6 - 6h - 14 - 6 + 14}}{{ - h}} = 6$
So left and write hand derivative are different so at $x = 1$ it is not derivative
So by definition we can say if $f(x)$ is not continuous and $g(x)$is a function of $f(x)$ in this case $g(x)$ is also discontinuous at these points. And if a function is not continuous at any point so the function is not derivable at these point
So $\sqrt 2 ,\sqrt 3 $ are point of discontinuity of $g(x)$ that mean it is not derivable at these point also
We know that $f(x)$ is discontinuous at $x = 2$ but we can not include because queation ask point of not differentiability in between \[\left( { - \dfrac{1}{2},2} \right)\]
So $g$ is NOT differentiable exactly at four point in \[\left( { - \dfrac{1}{2},2} \right)\]
Point where $g(x)$ is not differentiable is
$x = \{ 0,1,\sqrt 2 ,\sqrt 3 \} $

Therefore, option (B) and (C) are correct.

Note:
The differentiability of a function can be found by making a graph.
And differentiability of a function at the boundary point can be found by using one hand derivative either left or right hand.