Question

Let \[f\] be an odd function defined on the set of real numbers such that for \[x \geqslant 0\], \[f(x) = 3\sin x + 4\cos x\]. Then \[f(x)\] at \[x = \dfrac{{ - 11\pi }}{6}\] is equal to
A. \[\dfrac{{ - 3}}{2} - 2\sqrt 3 \]
B. \[\dfrac{3}{2} - 2\sqrt 3 \]
C. \[\dfrac{3}{2} + 2\sqrt 3 \]
D. \[\dfrac{{ - 3}}{2} + 2\sqrt 3 \]

Answer 1

Hint: Here we use the concept of odd functions which is \[f( - x) = - f(x)\] and solve for the value at given x. We break the angle in such a way that it is added or subtracted from \[2\pi \].

Complete step-by-step answer:
We have \[f(x) = 3\sin x + 4\cos x\]
Also, we know any function is an odd function if it satisfies \[f( - x) = - f(x)\].
Now we have to find the value of the function at point \[x = \dfrac{{ - 11\pi }}{6}\]
We have to find the value of \[f(\dfrac{{ - 11\pi }}{6})\]
Since, f is an odd function, therefore, we can use the concept \[f( - x) = - f(x)\]. Substitute \[x = \dfrac{{ - 11\pi }}{6}\].
\[ \Rightarrow f(\dfrac{{ - 11\pi }}{6}) = - f(\dfrac{{11\pi }}{6})\]
Now we can break the angle inside the function as
\[ \Rightarrow \dfrac{{11\pi }}{6} = \dfrac{{12\pi - \pi }}{6}\]
Separating the fraction into two parts
\[ \Rightarrow \dfrac{{11\pi }}{6} = \dfrac{{12\pi }}{6} - \dfrac{\pi }{6}\]
Cancel out common factors from numerator and denominator
\[ \Rightarrow \dfrac{{11\pi }}{6} = 2\pi - \dfrac{\pi }{6}\]
Therefore, we can write
\[f(\dfrac{{ - 11\pi }}{6}) = - f(2\pi - \dfrac{\pi }{6})\]
Now we know \[f(x) = 3\sin x + 4\cos x\]
Put \[x = 2\pi - \dfrac{\pi }{6}\]
\[ \Rightarrow f(\dfrac{{11\pi }}{6}) = 3\sin \left( {2\pi - \dfrac{\pi }{6}} \right) + 4\cos \left( {2\pi - \dfrac{\pi }{6}} \right)\] … (1)
Now we will use the quadrant graph to convert the angles.

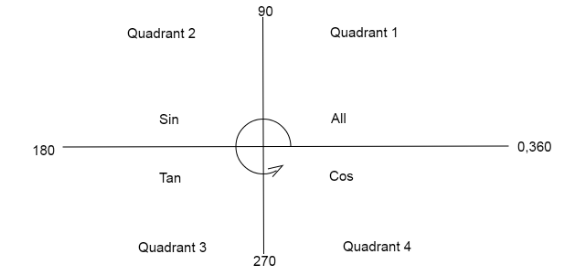
Here we denote \[2\pi = {360^ \circ },\pi = {180^ \circ }\]
Now we calculate the values of both the functions on RHS of the equation using the quadrant diagram.
For \[\sin \left( {2\pi - \dfrac{\pi }{6}} \right)\], we are subtracting from \[2\pi \]which goes into the fourth quadrant where sin function is negative.
So, the value of \[\sin \left( {2\pi - \dfrac{\pi }{6}} \right) = - \sin (\dfrac{\pi }{6}) = - \dfrac{1}{2}\] … (2)
For \[\cos \left( {2\pi - \dfrac{\pi }{6}} \right)\], we are subtracting from \[2\pi \]which goes into the fourth quadrant where the cos function is positive.
So, the value of \[\cos \left( {2\pi - \dfrac{\pi }{6}} \right) = \cos (\dfrac{\pi }{6}) = \dfrac{{\sqrt 3 }}{2}\] … (3)
Substitute the values from equation (2) and equation (3) in equation (1)
\[ \Rightarrow f(x) = 3(\dfrac{{ - 1}}{2}) + 4(\dfrac{{\sqrt 3 }}{2})\]
Multiply the terms in the bracket.
\[
   \Rightarrow f(\dfrac{{11\pi }}{6}) = \dfrac{{ - 3}}{2} + \dfrac{{4\sqrt 3 }}{2} \\
   \Rightarrow f(\dfrac{{11\pi }}{6}) = \dfrac{{ - 3}}{2} + 2\sqrt 3 \\
 \]
So now \[f( - \dfrac{{11\pi }}{6}) = - f(\dfrac{{11\pi }}{6})\]
Therefore,
\[
   \Rightarrow f( - \dfrac{{11\pi }}{6}) = - [\dfrac{{ - 3}}{2} + 2\sqrt 3 ] \\
   \Rightarrow f( - \dfrac{{11\pi }}{6}) = \dfrac{3}{2} - 2\sqrt 3 \\
 \]
So, option B is correct.

Note: Students are likely to make mistakes while calculating the values from the quadrant diagram, keep in mind that we always move anti-clockwise as we add the angles, so when we subtract the angle we move backwards or clockwise to see which quadrant our function lies in.