Question

Let \[{\text{f : [0,1] }} \to {\text{ R}}\](the set of all real numbers) be a function. Suppose the function f is twice differentiable, f(0) = f(1) = 0 and satisfies \[{\text{f ''}}\left( {\text{x}} \right){\text{ - 2f '}}\left( {\text{x}} \right){\text{ + f}}\left( {\text{x}} \right) \geqslant {{\text{e}}^{\text{x}}}{\text{, x}} \in {\text{[0,1]}}\] which of the following is true for 0 < x < 1 ?
$
  {\text{A}}{\text{. 0 < f(x) < }}\infty \\
  {\text{B}}{\text{. - }}\dfrac{1}{2} < {\text{f(x) < }}\dfrac{1}{2} \\
  {\text{C}}{\text{. - }}\dfrac{1}{4} < {\text{f(x) < 1}} \\
  {\text{D}}{\text{. - }}\infty {\text{ < f}}\left( x \right) < 0 \\
 $

Answer 1

Hint: Multiply the expression \[{\text{f ''}}\left( {\text{x}} \right){\text{ - 2f '}}\left( {\text{x}} \right){\text{ + f}}\left( {\text{x}} \right) \geqslant {{\text{e}}^{\text{x}}}\] by ${e^{ - x}}$ and then proceed with the calculations. Our main aim is to find the range of f(x) and in order to do that, find the concavity of the function obtained after certain calculative steps.

Complete step-by-step answer:
The given function f(x) is twice differentiable.
f(0) = f(1) = 0
Also, \[{\text{f ''}}\left( {\text{x}} \right){\text{ - 2f '}}\left( {\text{x}} \right){\text{ + f}}\left( {\text{x}} \right) \geqslant {{\text{e}}^{\text{x}}}{\text{, x}} \in {\text{[0,1]}}\]
Multiply the above expression by ${e^{ - x}}$. This gives us-
$
  {\text{f ''}}\left( {\text{x}} \right){\text{.}}{{\text{e}}^{ - x}}{\text{ - 2f '}}\left( {\text{x}} \right){\text{.}}{{\text{e}}^{ - x}}{\text{ + f}}\left( {\text{x}} \right).{e^{ - x}} \geqslant {{\text{e}}^{\text{x}}}{\text{.}}{{\text{e}}^{ - x}} \\
  {\text{f ''}}\left( {\text{x}} \right){\text{.}}{{\text{e}}^{ - x}}{\text{ - 2f '}}\left( {\text{x}} \right){\text{.}}{{\text{e}}^{ - x}}{\text{ + f}}\left( {\text{x}} \right).{e^{ - x}} \geqslant 1 \\
  {\text{f ''}}\left( {\text{x}} \right){\text{.}}{{\text{e}}^{ - x}}{\text{ - f '}}\left( {\text{x}} \right){\text{.}}{{\text{e}}^{ - x}}{\text{ - f '(x)}}{\text{.}}{{\text{e}}^{ - x}}{\text{ + f}}\left( {\text{x}} \right).{e^{ - x}} \geqslant 1 \\
  \dfrac{{d\left( {f'(x).{e^{ - x}}} \right)}}{{dx}} - \dfrac{{d\left( {f'(x).{e^{ - x}}} \right)}}{{dx}} \geqslant 1 \\
  \dfrac{{d\left( {f'(x).{e^{ - x}} - f\left( x \right).{e^{ - x}}} \right)}}{{dx}} \geqslant 1......eq\left( 1 \right) \\
  {\text{The expression }}\left( {f'(x).{e^{ - x}} - f\left( x \right).{e^{ - x}}} \right){\text{ can also be written as}} \\
  \dfrac{{d\left( {f\left( x \right).{e^{ - x}}} \right)}}{{dx}} \\
  {\text{The eq}}{\text{. 1 becomes - }} \\
  \dfrac{{{d^2}\left( {f\left( x \right).{e^{ - x}}} \right)}}{{dx}} \geqslant 1 \\
$
Now since the double derivative of $f\left( x \right).{e^{ - x}}$ is greater than 1 it implies that it is greater than 0 as well. Hence, the function $f\left( x \right).{e^{ - x}}$is concave upwards. Let the function $f\left( x \right).{e^{ - x}}$ be g(x), for easy reference.
It is given that f(0) = f(1) = 0. This gives
g(0) = g(1) = 0.
The information collected about g(x) is-
It is concave upwards
g(0) = g(1) = 0

When we plot g(x), it should look like-

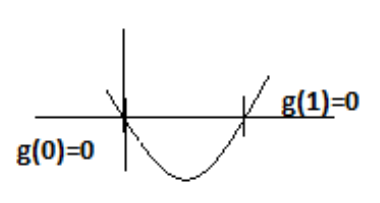
In the interval 0 to 1- g(x) is less than 0.
g(x)<0
f(x).e-x<0
we know that e-x is always greater than 0 that means it is an all time positive term. Hence it is f(x) which makes f(x).e-x a negative erm.
Thus, f(x) < 0.
So, the option D is correct.

Note: Whenever the range of a function is asked, try to plot the curve if possible. Since we could not draw the f(x) the derivative expression was multiplied by a factor of e-x because we know the nature of the curve. So, it was easier to derive conclusions in the end.