Question

Let \[\Delta XOY\]be a right angled triangle\[\angle XOY = {90^ \circ }\]. Let \[M\]and \[N\]be the midpoints of legs \[OX\]and \[OY\] respectively. Given that \[XN = 19\]and \[YM = 22\], the length \[XY\]is equal to?

Answer 1

Hint: Construct the triangle carefully and accordingly as instructed. Use the fact of having the right angle triangle. Use the property of Pythagoras theorem if applicable to get the length of the side \[XY\] of the triangle \[\Delta XOY\]

Complete step-by-step solution:

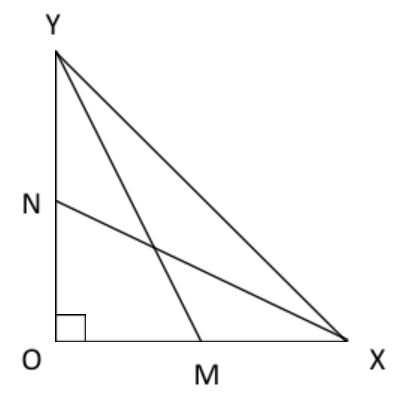
We are given that \[\Delta XOY\]be a right angled triangle\[\angle XOY = {90^ \circ }\]. Let \[M\]and \[N\]be the midpoints of legs \[OX\]and \[OY\] respectively such that \[XN = 19\]and \[YM = 22\].
Let us consider the \[\Delta MOY\]such that \[OM{\kern 1pt} = x\]and \[ON{\kern 1pt} = y\]with \[\angle MOY = {90^ \circ }\]and \[\Delta XON\]such that \[OX{\kern 1pt} = 2x\]and \[OY{\kern 1pt} = 2y\]
Now using Pythagoras theorem on both these triangles we have,
In\[\Delta MOY\],\[M{O^2} + O{Y^2} = M{Y^2}\]
\[ \Rightarrow {x^2} + {(2y)^2} = {22^2}\]
\[ \Rightarrow {x^2} + 4{y^2} = 484\] ------------\[(1)\]
In\[\Delta XON\],\[X{O^2} + O{N^2} = X{N^2}\]
\[ \Rightarrow {(2x)^2} + {y^2} = {19^2}\]
\[ \Rightarrow 4{x^2} + {y^2} = 361\] -------------\[(2)\]
Summing equations \[(1)\]and \[(2)\]we have,
\[5{x^2} + 5{y^2} = 845\]
\[ \Rightarrow {x^2} + {y^2} = 169\] ------------\[(3)\]
Again in \[\Delta XOY\]using Pythagoras theorem we have,
\[X{O^2} + O{Y^2} = X{Y^2}\]
\[
   \Rightarrow {(2x)^2} + {(2y)^2} = X{Y^2} \\
   \Rightarrow 4{x^2} + 4{y^2} = X{Y^2} \\
 \]
\[ \Rightarrow 4({x^2} + {y^2}) = X{Y^2}\]
From equation \[(3)\]we have,
\[
   \Rightarrow 4(169) = X{Y^2} \\
   \Rightarrow XY = \sqrt {4\times 169} \\
   \Rightarrow XY = 2\times 13 \\
   \Rightarrow XY = 26 \]
Hence we have that the length of \[XY\] is equal to \[26\]units.
Additional information: In Geometry, a triangle is a three-sided polygon that includes \[3\] edges and \[3\] vertices. The maximum crucial assets of a triangle are that the sum of the internal angles of a triangle is identical to a hundred and eighty degrees. This asset is known as the angle sum property of a triangle. According to Pythagoras, the length of the hypotenuse is identical to the sum of the squares of the alternative facets of a triangle. Triangle is a closed two-dimensional shape. It is a three-sided polygon. All facets are made of perfect straight lines. The point in which two edges meet is the vertex. Hence, the triangle has \[3\] vertices each vertex with an angle.

Note: It is important that we analyze the diagram of the triangle carefully and read the given conditions properly. It is also important that we keep in mind that the triangle is a right angled triangle and this itself should give us an intuition that we can use Pythagoras Theorem.