Question

Let \[\Delta PQR\] be a right angled isosceles triangle right angled at \[P = \left( {2,1} \right)\]. If the equation of the line \[QR\] is \[2x + y = 3\], then the equation representing the pair of lines \[PQ\] and \[PR\] is
\[\left( 1 \right)\] \[3{x^2} - 3{y^2} + 8xy + 20x + 10y + 25 = 0\]
\[\left( 2 \right)\] \[3{x^2} - 3{y^2} + 8xy - 20x - 10y + 25 = 0\]
\[\left( 3 \right)\] \[3{x^2} - 3{y^2} + 8xy + 10x + 15y + 20 = 0\]
\[\left( 4 \right)\] \[3{x^2} - 3{y^2} - 8xy - 10x - 15y - 20 = 0\]

Answer 1

Hint: We have to find the expression of the product of the two equations of the side of the triangle. We solve this question using the concept of the formation of the equation of a line, the concept of slope of a line. We should have the knowledge about the formula for finding the value of the slope of a line using the equation of the line. We should also have the knowledge about the formula of the relation of the two slopes. First, we will find the slope of the given line and then using the concept of slope, we will find the slope of the perpendicular lines and then using the formula of relation between two slopes, we will find the equations of the respective lines and then multiplying both the equations we will find the required expression for the pair of lines \[PQ\] and \[PR\].

Complete step-by-step solution:
Given:
\[P = \left( {2,1} \right)\]
The equation of the line \[QR\] is \[2x + y = 3\]
Construct: The figure is as shown.

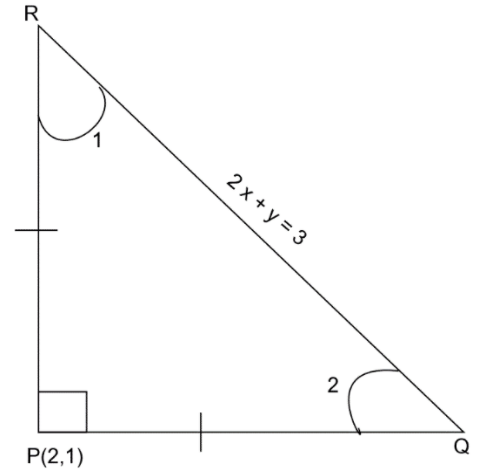
We know that the equation of a line is given as:
\[y = mx + c\]
Where \[m\] is the slope of the equation of line.
Now, we can write the equation of line as:
\[y = - 2x + 3\]
So, on comparing the two equations we get the value of slope as:
\[m = - 2\]
Let us consider that the slope of \[PR\] be \[{m_1}\] and slope of \[PQ\] be \[{m_2}\].
Also, we know that the property of slope of perpendicular lines is given as:
\[{m_1} \times {m_2} = - 1\]
So, we get the slope of \[PQ\] as:
\[{m_2} = \dfrac{{ - 1}}{{{m_1}}}\]
As the \[\Delta PQR\] is a right angled isosceles triangle.
Then, \[\angle 1 = \angle 2\]
Angles opposite equal sides are always equal.
So, we get the value of both angles as:
\[\angle 1 + \angle 2 + {90^\circ } = {180^\circ }\]
\[2\angle 1 = {90^\circ }\]
The value of both angles is:
\[\angle 1 = \angle 2 = {45^\circ }\]
Now, we also know that the slope of two lines is given as:
\[\tan \theta = \left| {\dfrac{{{m_1} - {m_2}}}{{1 + {m_1}{m_2}}}} \right|\]
Where \[\theta \] is the angle between the two lines.
Hence, using the formula we can write the expression as:
\[\tan {\angle 1} = \left| {\dfrac{{{m_1} - \left( { - 2} \right)}}{{1 + {m_1}\left( { - 2} \right)}}} \right|\]
\[\tan {45^\circ } = \left| {\dfrac{{{m_1} + 2}}{{1 - 2{m_1}}}} \right|\]
As, we know that the value of \[\tan {45^\circ } = 1\].
Putting the values, we get the expression as:
\[1 = \left| {\dfrac{{{m_1} + 2}}{{1 - 2{m_1}}}} \right|\]
\[{m_1} + 2 = \left| {1 - 2{m_1}} \right|\]
Splitting the modulus function, we get the expression as:
\[{m_1} + 2 = \pm \left( {1 - 2{m_1}} \right)\]
Taking the two cases, we get the value of slope as:
\[{m_1} + 2 = 1 - 2{m_1}\] or \[{m_1} + 2 = - 1 + 2{m_1}\]
On solving we get the two values of slope as:
\[{m_1} = \dfrac{{ - 1}}{3}\] or \[{m_1} = 3\]
Also, we know that the formula for one point form of line is given as:
\[\left( {y - {y_1}} \right) = m\left( {x - {x_1}} \right)\]
Where \[m\] is the slope of the line and \[\left( {{x_1},{y_1}} \right)\] is the point on the line.
\[P = \left( {2,1} \right)\]
Taking two cases, we get the equations of the lines as:
\[case1:\]
\[{m_1} = \dfrac{{ - 1}}{3}\]
We get the equation of line as:
\[\left( {y - 1} \right) = \dfrac{{ - 1}}{3}\left( {x - 2} \right)\]
\[3\left( {y - 1} \right) = - 1\left( {x - 2} \right)\]
On simplifying, we get the equation of line as:
\[3y - 3 = - x + 2\]
\[3y + x - 5 = 0\]
\[case2:\]
\[{m_1} = 3\]
We get the equation of line as:
\[\left( {y - 1} \right) = 3\left( {x - 2} \right)\]
\[y - 1 = 3x - 6\]
On simplifying, we get the equation of line as:
\[3x - y - 5 = 0\]
Now, the product of the equations is given as:
\[\left( {3x - y - 5} \right)\left( {3y + x - 5} \right) = 0\]
Now expanding the terms, we get
\[9xy - 3{y^2} - 15y + 3{x^2} - xy - 5x - 15x + 5y + 25 = 0\]
\[3{x^2} - 3{y^2} + 8xy - 10y - 20x + 25 = 0\]
Hence, the equation representing the pair of lines \[PQ\] and \[PR\] is \[3{x^2} - 3{y^2} + 8xy - 10y - 20x + 25 = 0\].
Thus, the correct option is \[\left( 2 \right)\].

Note: We have various different formulas for the equation of line like the slope intercept form, two point form. We also have various formulas for the slope of an equation. We use the particular formula seeing the type of data which is given.
The slope can also be given as:
\[slope = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\]