Question

Let $ \cos (\alpha + \beta ) = $ $ \dfrac{4}{5} $ and let $ \sin (\alpha - \beta ) = $ $ \dfrac{5}{{13}} $ , where 0 ≤ α, β ≤ $ \dfrac{\pi }{4} $ , then $ \tan 2\alpha $ is equal to
A. $ \dfrac{{20}}{7} $
B. \[\dfrac{{25}}{{16}}\]
C. $ \dfrac{{56}}{{33}} $
D. $ \dfrac{{19}}{{12}} $

Answer 1

Hint: We know the cosine of any angle is the ratio of the base to hypotenuse in a right angled triangle. Similarly, sine of any angle is the ratio of the opposite side to hypotenuse in a right angled triangle. Further, we will use Pythagoras theorem to calculate the other trigonometry ratio which is $ \tan 2\alpha $ .
Formula Used: The following formula is used to get to the final answer,
 $ \tan (\alpha + \beta ) = $ $ \dfrac{{\tan \alpha + \tan \beta }}{{1 - \tan \alpha \tan \beta }} $

Complete step-by-step answer:
According to the given information, we have
The first function is $ \cos (\alpha + \beta ) = $ $ \dfrac{4}{5} $

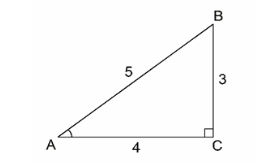
Also, we know $ \cos (\alpha + \beta ) = \dfrac{4}{5} $
Therefore take the base to be 4k and hypotenuse as 5k, where k is a constant.
Further, perpendicular = $ \sqrt {{{(hypotenuse)}^2}\;-{\text{ }}{{\left( {base} \right)}^2}} $
 $ \Rightarrow \sqrt {{{(5k)}^2} - {{(4k)}^2}} $ $ = \sqrt {9{k^2}} $
Finally we get the perpendicular to be 3k.
Now for a right angled triangle ABC we know that,
 $ \tan (\alpha + \beta ) = $ $ \dfrac{3}{4} $ $ ...(1) $
The second function is $ \sin (\alpha - \beta ) = $ $ \dfrac{5}{{13}} $

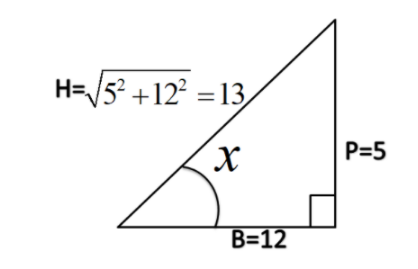
Also, we know $ \sin (\alpha - \beta ) = \dfrac{5}{{13}} $
Therefore, take the perpendicular to be 5k and hypotenuse as 13k, where k is a constant.
Further, base = $ \sqrt {{{(hypotenuse)}^2}\;-{\text{ }}{{\left( {perpendicular} \right)}^2}} $
 $ \Rightarrow \sqrt {{{(13k)}^2} - {{(5k)}^2}} $ $ = \sqrt {144{k^2}} $
Finally we get the base to be 12k.
Now for a right angled triangle ABC we know that,
Hence we get,
 $ \tan (\alpha - \beta ) = $ $ \dfrac{5}{{12}} $ $ ...(2) $
According to the given data,
The following formula is used to get,
 $ \tan (\alpha + \beta ) = $ $ \dfrac{{\tan \alpha + \tan \beta }}{{1 - \tan \alpha \tan \beta }} $
 $ \tan ((\alpha + \beta ) + (\alpha - \beta )) $ = $ \dfrac{{\tan (\alpha + \beta ) + \tan (\alpha - \beta )}}{{1 - \tan (\alpha + \beta )\tan (\alpha - \beta )}} $
On simplifying further we get,
 $ \tan 2\alpha $ $ = \dfrac{{\dfrac{3}{4} + \dfrac{5}{{12}}}}{{1 - \dfrac{3}{4} \times \dfrac{5}{{12}}}} $
 $ \Rightarrow \dfrac{{\dfrac{{36 + 20}}{{48}}}}{{\dfrac{{48 - 15}}{{48}}}} $ $ = \dfrac{{56}}{{33}} $
So, the correct answer is “$ \dfrac{{56}}{{33}} $ ”.

Note: In order to solve problems of this type the key is to have a basic understanding of trigonometric equations and values and also learn its implications. Students should be aware of applications of the trigonometric values in order to simplify the given equation.