Question

Let C be the circle with centre at $\left( {1,1} \right)$ and radius $ = 1$. If T is the circle centred at $\left( {0,y} \right)$, passing through origin and touching the circle C externally, then what is the radius of the circle T?
A) $\dfrac{{\sqrt 3 }}{{\sqrt 2 }}$
B) $\dfrac{{\sqrt 3 }}{2}$
C) $\dfrac{1}{2}$
D) $\dfrac{1}{4}$

Answer 1

Hint: We are given a circle C with centre at $\left( {1,1} \right)$ and radius = 1. Another circle T centred at $\left( {0,y} \right)$ is also given. We have to find the radius of the circle T. We are also given that this circle T touches the circle C externally and passes through the origin. Join the radii of the two circles. Then draw a line from T parallel to x-axis and a line from C parallel to y-axis. Let both the lines meet at a certain point. This will form a triangle. Use Pythagoras theorem to find the value of y.

Complete step-by-step solution:
In this question we are given a circle C with centre at $\left( {1,1} \right)$ and radius = 1. Another circle T centred at $\left( {0,y} \right)$ is also given. We have to find the radius of the circle T. We are also given that this circle T touches the circle C externally.
Let us draw a diagram first.

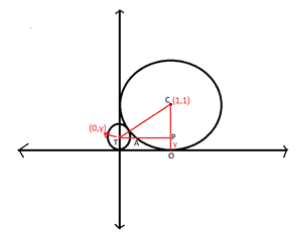
The centre of the bigger circle is C and that of the smaller circle is T. Draw a line from T parallel to x-axis and a line from C parallel to y-axis. Let both the lines meet at point P. Now we have a triangle, $\vartriangle CTP$. We will solve this question using Pythagoras theorem in $\vartriangle CTP$.
If we look closely in the figure, the coordinates of P is $\left( {1,y} \right)$.
$ \Rightarrow $$TP = 1$ unit (as the point P is perpendicularly below the point C whose x-coordinate is 1).
$ \Rightarrow PO = y$ (as the distance of point P from x-axis is equal to the radius of smaller circle)
Now, since $PO = y$, distance of $CP = \left( {1 - y} \right)$.
$ \Rightarrow CT = AC + AT$ (On looking closely, we will notice that AC is the radius of the bigger circle and AT is the radius of the smaller circle.)
Therefore, $AC = 1,AT = y$. Hence, $CT = \left( {1 + y} \right)$
Now since we have all the required distances, we can use Pythagoras theorem in $\vartriangle CTP$.
$ \Rightarrow {\left( {CT} \right)^2} = {\left( {CP} \right)^2} + {\left( {PT} \right)^2}$
Putting all the values,
$ \Rightarrow {\left( {1 + y} \right)^2} = {\left( {1 - y} \right)^2} + {1^2}$
Now we will solve for y,
$ \Rightarrow 1 + {y^2} + 2y = 1 + {y^2} - 2y + 1$
On simplifying we will get,
$ \Rightarrow 1 + {y^2} + 2y - 1 - {y^2} + 2y = 1$
$ \Rightarrow 4y = 1$
$ \Rightarrow y = \dfrac{1}{4}$
Now we have our y coordinate. Since our circle touches the origin, its radius will be equal to the y-coordinate.

Therefore, radius = option (D) $\dfrac{1}{4}$.

Note: This question can also be solved by distance formula on line CT. We have two points - $\left( {0,y} \right)$ and $\left( {1,1} \right)$. The distance between the points is $\left( {1 + y} \right)$ unit.
We know, $d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} $
Putting the values,
$ \Rightarrow 1 + y = \sqrt {{{\left( {1 - 0} \right)}^2} + {{\left( {1 - y} \right)}^2}} $
Squaring both the sides,
$ \Rightarrow {\left( {1 + y} \right)^2} = 1 + {\left( {1 - y} \right)^2}$
On solving we will get,
$ \Rightarrow 1 + 2y + {y^2} = 1 + 1 + {y^2} - 2y$
$ \Rightarrow 1 - 1 + 2y + 2y + {y^2} - {y^2} = 1$
$ \Rightarrow y = \dfrac{1}{4}$
Therefore, radius = $\dfrac{1}{4}$