Question

Let \[A\left( {2, - 3} \right)\]and \[B\left( { - 2,1} \right)\] be two angular points of \[\Delta ABC\]. If the centroid of the triangle moves on the line \[2x + 3y = 1\], then the locus of the angular point \[C\] is given by:

Answer 1

Hint: The centroid of a two-dimensional figure, the "triangle" is obtained by intersecting all three of its medians. A locus is a group of points that satisfy some geometrical condition. And the locus equation is an equation that is fulfilled by all the points in the problem that fulfill the given geometrical condition. When two lines are parallel only their constant term will differ.

Complete step-by-step answer:
Let us first note down the given values;
The question tells us about two of the corners \[A,B\] are \[A\left( {2, - 3} \right)\]and \[B\left( { - 2,1} \right)\]
The equation of the line on which the centroid, say $G$ lies on is: \[2x + 3y = 1\]
Look at the figure given below:

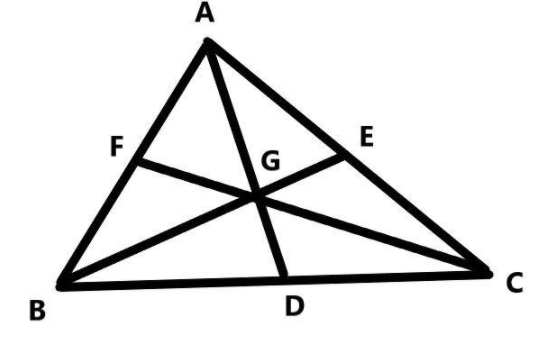
The lines drawn from each corner to the center of the opposite edge are said to be the median of a triangle and here $AD,\;BE$ and $CF$ are the medians constructed. They have intersected at a point $G$ which is named as the centroid of the given triangle.
Now we move on to solving the problem;
Let us consider the two of the points which are already given:
\[A\left( {2, - 3} \right)\]and \[B\left( { - 2,1} \right)\]
Next we can represent the third point as:
$C(\alpha ,\beta )$
Then the centroid $G$ of the constructed triangle will be:
$ \Rightarrow G = (\dfrac{{sum\;of\;x - coordinates}}{3},\dfrac{{sum\;of\;y - coordinates}}{3})$
$ \Rightarrow G = (\dfrac{{2 - 2 + \alpha }}{3},\dfrac{{ - 3 + 1 + \beta }}{3})$
$ \Rightarrow G = (\dfrac{\alpha }{3},\dfrac{{\beta - 2}}{3})$ are coordinates of the centroid in terms of the third point of the triangle.
But we are also given that the centroid moves along the line:
\[2x + 3y = 1\]
So the equation of locus will finally be of this form:
\[2x + 3y = q\], because the ‘line on which centroid is present’ and ‘the locus of the point $C$’ are parallel to each other.
Now we should be clear that the equation of any line which is parallel to another line will have the same linear equation and only have a difference in the constant of that equation.
Take note that every point that lies on any given line will satisfy the equation of that line also.
The coordinates of centroid, in terms of $C$ will also satisfy this equation: \[2x + 3y = 1\], because the centroid lies on it.
So substituting $G = (\dfrac{\alpha }{3},\dfrac{{\beta - 2}}{3})$ in place of $(x,y)$ in the equation \[2x + 3y = 1\]
$ \Rightarrow 2(\dfrac{\alpha }{3}) + 3(\dfrac{{\beta - 2}}{3}) = 1$
On simplifying we get the equation to be:
$ \Rightarrow 2\alpha + 3\beta = 9$
On comparing this equation with the equation of the line parallel to it, can be written in this way;
$ \Rightarrow 2x + 3y = 9$
Therefore finally the equation of the required locus of point $C$ is: $2x + 3y = 9$.
So, the correct answer is “ $2x + 3y = 9$”.

Note: Centroids are used in the following applications: - In architecture to properly align structures with minimal stress. Also the centroid of a triangle could be useful in determining the core center of a certain location. Take an example, if anyone wants to build a swimming pool at the center of a neighborhood, they must first determine where the center of that neighborhood is situated.