Question

Let ABCDEF be a regular hexagon in the x – y plane and $\vec A\vec B = 4\hat i$, then $\vec C\vec D$ is equal to
$\left( a \right)6\hat i + 2\sqrt 3 \hat j$
$\left( b \right)2\left( { - \hat i + \sqrt 3 \hat j} \right)$
$\left( c \right)2\left( {\hat i + \sqrt 3 \hat j} \right)$
$\left( d \right)2\left( {\hat i - \sqrt 3 \hat j} \right)$

Answer 1

Hint: In this particular question use the concept that in a regular hexagon the length of all sides is the equal only difference is the direction assume AB be the reference direction i.e. AB on the positive x-axis and use the concept that the internal angle of a regular hexagon is always 120 degrees, so use these concepts to reach the solution of the question.

Complete step-by-step solution:

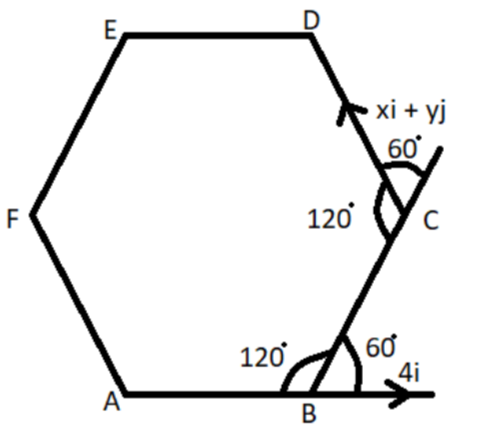
ABCDEF regular hexagon is shown above in the diagram.
Let AB be the reference, and it is given that $\vec A\vec B = 4\hat i$
Now we have to find out the $\vec C\vec D$ as shown in the above figure.
Let, $\vec C\vec D = x\hat i + y\hat j$
Now as we know that in a regular hexagon the length of all sides is equal i.e. magnitude of the sides is equal.
$ \Rightarrow \left| {\vec A\vec B} \right| = \left| {\vec C\vec D} \right|$
$ \Rightarrow \left| {4\hat i} \right| = \left| {x\hat i + y\hat j} \right|$
Now as we know that $\left| {x\hat i + y\hat j} \right| = \sqrt {{x^2} + {y^2}} $ so use this property in the above equation we have,
$ \Rightarrow \sqrt {{4^2} + {0^2}} = \sqrt {{x^2} + {y^2}} $
Now take square root on both sides we have,
$ \Rightarrow {4^2} = {x^2} + {y^2}$..................... (1)
Now as we know that the internal angle of a regular hexagon is always 120 degrees as shown in the above figure.
$ \Rightarrow \angle ABC = {120^o}$
So the angle line BC makes with the positive direction of x axis is,
$ \Rightarrow {180^o} - {120^o} = {60^o}$
So the line CD makes an angle $\left( {{{60}^o} + {{60}^o}} \right) = {120^o}$ with the positive direction of x axis.
So the slope of the line CD is, $\tan {120^o} = - \sqrt 3 $.............. (2)
But, $\vec C\vec D = x\hat i + y\hat j$
And the slope of the above equation is,
$\tan \theta = \dfrac{y}{x}$................ (3)
Now (2) and (3) both are the same so equate them we have,
$ \Rightarrow \dfrac{y}{x} = - \sqrt 3 $
$ \Rightarrow y = - x\sqrt 3 $............... (4)
Now substitute this value in equation (1) we have,
$ \Rightarrow {4^2} = {x^2} + {\left( { - x\sqrt 3 } \right)^2}$
$ \Rightarrow {4^2} = {x^2} + 3{x^2}$
$ \Rightarrow 4{x^2} = 16$
$ \Rightarrow {x^2} = 4$
$ \Rightarrow x = \pm 2$
Now as the direction of the line CD is 120 degrees with the positive direction of the x-axis so the line lies in the second quadrant, and in the second quadrant x is negative and y is positive.
Therefore, x = -2
Now substitute this value in equation (4) we have,
$ \Rightarrow y = 2\sqrt 3 $
So the vector CD becomes
$ \Rightarrow \vec C\vec D = - 2\hat i + 2\sqrt 3 \hat j = 2\left( { - \hat i + \sqrt 3 \hat j} \right)$
So this is the required vector.
Hence option (b) is the correct answer.

Note: Whenever we face such types of questions the key concept we have to remember is that always recall that after 120-degree rotation with the reference in anti-clockwise the vector goes into the second quadrant and in the second quadrant the value of x is negative and the value of y is positive so chose the values of x and y during calculation according to this as above chosen.