Question

Let ABCD be a square of side 2a. Find the coordinates of the vertices of this square when (i) A coincides with the origin and AB and AD are along OX and OY respectively. (ii) The centre of the square is at the origin and coordinate axes are parallel to the sides AB and AD respectively.

Answer 1

Hint: For solving this question, we should be aware about the basics of graph plotting. X-direction means going towards right while Y-direction means going upwards. Further, going left means going in the negative direction of X while going downwards means going in the negative direction of Y-axis. Apart from this we will use the basic terminology of Cartesian coordinates like the origin, x and y axis to solve the problem.

Complete step by step answer:
 (i) To solve this part, we will refer to the figure below.

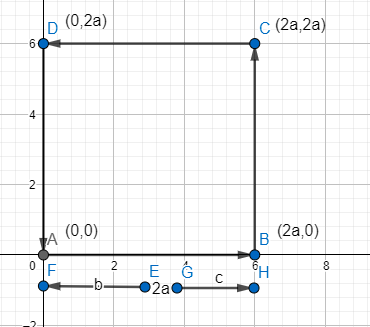
It is given that point A coincides with the origin, thus co-ordinate of A is (0,0). Further, it is also given that and AB and AD are along OX and OY respectively (OX is X-axis and OY is Y-axis), thus point B is given by (0+2a,0) = (2a,0) and point D is given by (0,0+2a) = (0,2a). This is because the edge length of the square in the problem is 2a and we have to move along the X-axis and Y-axis respectively. To find point C, we can see from the figure that we have to go vertically upwards from point B. Thus, y coordinate gets altered by 2a. Thus, we have coordinates of point C as (2a,0+2a) = (2a,2a)
(ii) To solve this part, we will refer to the figure below.

It is given that centre coincides with the origin, thus coordinate of centre is (0,0). Further, it is also given that AB and AD are along OX and OY respectively (OX is X-axis and OY is Y-axis), thus to get point B, we move towards the right from the centre by a unit and then downwards by a unit. Thus, B co-ordinate is (0+a,0-a) = (a, -a). Now, to get point C, we move towards the right from the centre by a unit and then upwards by a unit. Thus, C co-ordinate is (0+a,0+a) = (a, a). Now, to get point A, we move towards the left from the centre by a unit and then downwards by a unit. Thus, A coordinate is (0-a,0-a) = (-a, -a). Now, to get point D, we move towards the left from the centre by a unit and then upwards by a unit. Thus, D co-ordinate is (0-a,0+a) = (-a, a).

Note: Plotting on the graph is generally helpful in various questions like those involving geometry where plotting on a graph paper can greatly simplify the understanding of the geometry problem. In this case, we dealt with squares, however, we can represent almost any figure on the Cartesian plane (example includes triangle, rectangle, etc.) and then solve the problem.