Question

Let $ABC$ be an equilateral triangle inscribed in a circle $O$ . $M$ is a point on the arc $BC$ . Lines $AM,BM$ and $CM$ are drawn. Then $\mathop {AM}\limits^{\_\_\_\_\_} $ is:
$\left( a \right){\text{ equal to }}\mathop {BM}\limits^{\_\_\_\_\_} + \mathop {CM}\limits^{\_\_\_\_\_} $

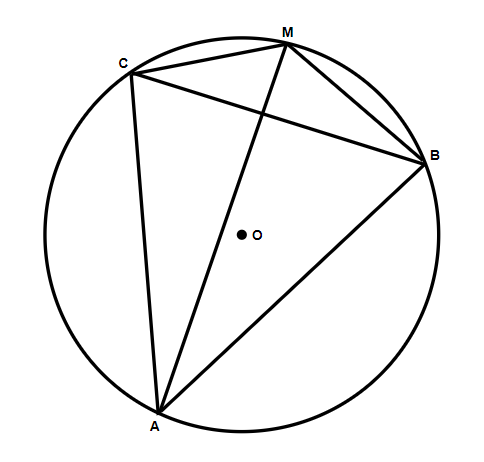
$\left( b \right){\text{ less than }}\mathop {BM}\limits^{\_\_\_\_\_} + \mathop {CM}\limits^{\_\_\_\_\_} $
$\left( c \right){\text{ greater than }}\mathop {BM}\limits^{\_\_\_\_\_} + \mathop {CM}\limits^{\_\_\_\_\_} $
$\left( d \right){\text{ equal, less than, or greater than }}\mathop {BM}\limits^{\_\_\_\_\_} + \mathop {CM}\limits^{\_\_\_\_\_} ,{\text{ depending upon position upon M}}$

Answer 1

Hint: For proving this type of question, all we can do is proceed with the information and figure provided. So we can see that since the $O$ is the center which lies on $AM$ hence, $AM$ will be equal to $2R$. And also $AM$ is perpendicular to $BC$ and also $AD$ is perpendicular to the same. So by using this we will equate both of them and get the value. And on solving it we will be able to find the required equation.

Complete answer:
First of all, we will assume this is an ideal case. And since, from the information provided, we can say that $O$ is the center which lies on $AM$ .
Therefore, $AM = 2R$ and here $R$ will be the radius of the circle.
Also, we can see that $AM \bot BC$ , so from this $O$ will be the point which lies on $AM$ and $BC$ .
Here, $AD \bot BC$ , so from the figure we can write it in fraction as
$ \Rightarrow \dfrac{{BD}}{{OB}} = \dfrac{{\sqrt 3 }}{2}$
Now let us assume $AB = BC = CA = a{\text{ , OA = OB = OC = R}}$
Therefore, on substituting the values, we will get the relation as
$ \Rightarrow \dfrac{a}{{2R}} = \dfrac{{\sqrt 3 }}{2}$
And by doing the cross multiplication and solving the above equation, we get the equation as
$ \Rightarrow a = \sqrt 3 R$
Since, we have $AM = 2R$ ,
So by using the trigonometric properties, we have
$ \Rightarrow BM = CM = \dfrac{{BD}}{{\cos {{30}^ \circ }}}$
And on solving the above line, we get the equation as
$ \Rightarrow \dfrac{a}{{\sqrt 3 }}$
So from this now we can have the sum of $BM\& CM$
On adding the sum, we will get $\dfrac{{2a}}{{\sqrt 3 }}$
Now on substituting the value of $a$ , we get the equation as
$ \Rightarrow \dfrac{{2 \times \sqrt 3 R}}{{\sqrt 3 }}$
And on solving the above line we get
$ \Rightarrow 2R = AM$
Therefore, from this, we can say \[\mathop {AM}\limits^{\_\_\_\_\_} = \mathop {BM}\limits^{\_\_\_\_\_} + \mathop {CM}\limits^{\_\_\_\_\_} \] .

Hence, the option $\left( a \right)$ is correct.

Note: For solving this type of question we need to know the geometry and its properties ideas so that we can equate the equation. Also, the use of trigonometry should be known to us as they are used sometimes. So by using the relation we will expand the equation and solve it then we can easily get to the solution.