
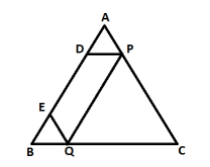
Let ABC be a triangle and D and E be two points on side AB such that AD = BE. If $DP\parallel BC$ and $EQ\parallel AC$, then prove that $PQ\parallel AB$.

Answer
563.7k+ views
Hint: Let’s recall the theorem of basic proportionality, also known as Thales theorem. The theorem states that, if a line is drawn parallel to one side of the triangle intersecting the other two sides, then the line cuts the sides of a triangle in the same ratio. Here, ABC is a triangle with two points D and E on side AB. Given that, $DP\parallel BC$ and $EQ\parallel AC$. Therefore, by theorem of basic proportionality, $\dfrac{{AD}}{{DB}} = \dfrac{{AP}}{{PC}}$ and $\dfrac{{BE}}{{EA}} = \dfrac{{BQ}}{{QC}}$. Now, AD = BE , given. Therefore equate these relations and proceed.
Complete step-by-step solution:
Let us recall the theorem of basic proportionality, also known as Thales theorem. The theorem states that, if a line is drawn parallel to one side of the triangle intersecting the other two sides, then the line cuts the sides of a triangle in the same ratio.
Now, given that ABC is a triangle with two points D and E on side AB.
Also, $DP\parallel BC$
Therefore, by theorem of basic proportionality, we have $\dfrac{{AD}}{{DB}} = \dfrac{{AP}}{{PC}}$ ……….…(1)
Again, $EQ\parallel AC$
Therefore, $\dfrac{{BE}}{{EA}} = \dfrac{{BQ}}{{QC}}$ ……….…(2)
Now, AD = BE , given.
$\Rightarrow$ AD + DE = BE + DE
$\Rightarrow$ EA = BD
Now, substituting AD with BE and BD with EA in equation (1), we get
$\dfrac{{AD}}{{DB}} = \dfrac{{BE}}{{EA}} = \dfrac{{AP}}{{PC}} = \dfrac{{BQ}}{{QC}}$
$\Rightarrow$ $\dfrac{{AP}}{{PC}} = \dfrac{{BQ}}{{QC}}$
$\Rightarrow$ P and Q divide the sides of the triangle ABC in the same ratio.
Therefore, by the converse of the theorem of basic proportionality, we have $PQ\parallel AB$.
Note: The theorem of basic proportionality is also known as Thales theorem. The theorem states that, if a line is drawn parallel to one side of the triangle intersecting the other two sides, then the line cuts the sides of a triangle in the same ratio.
Complete step-by-step solution:
Let us recall the theorem of basic proportionality, also known as Thales theorem. The theorem states that, if a line is drawn parallel to one side of the triangle intersecting the other two sides, then the line cuts the sides of a triangle in the same ratio.

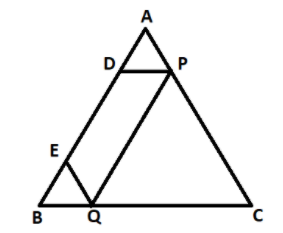
Now, given that ABC is a triangle with two points D and E on side AB.
Also, $DP\parallel BC$
Therefore, by theorem of basic proportionality, we have $\dfrac{{AD}}{{DB}} = \dfrac{{AP}}{{PC}}$ ……….…(1)
Again, $EQ\parallel AC$
Therefore, $\dfrac{{BE}}{{EA}} = \dfrac{{BQ}}{{QC}}$ ……….…(2)
Now, AD = BE , given.
$\Rightarrow$ AD + DE = BE + DE
$\Rightarrow$ EA = BD
Now, substituting AD with BE and BD with EA in equation (1), we get
$\dfrac{{AD}}{{DB}} = \dfrac{{BE}}{{EA}} = \dfrac{{AP}}{{PC}} = \dfrac{{BQ}}{{QC}}$
$\Rightarrow$ $\dfrac{{AP}}{{PC}} = \dfrac{{BQ}}{{QC}}$
$\Rightarrow$ P and Q divide the sides of the triangle ABC in the same ratio.
Therefore, by the converse of the theorem of basic proportionality, we have $PQ\parallel AB$.
Note: The theorem of basic proportionality is also known as Thales theorem. The theorem states that, if a line is drawn parallel to one side of the triangle intersecting the other two sides, then the line cuts the sides of a triangle in the same ratio.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Who is eligible for RTE class 9 social science CBSE

Which places in India experience sunrise first and class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE




