Question

Let $ABC$ as an equilateral triangle of side $2a$. Find each of its altitudes
1) $a\sqrt 3 $
2) $2a\sqrt 3 $
3) $a\sqrt 2 $
4) $a\sqrt 6 $

Answer 1

Hint: We will first draw the diagram from the given conditions. We will get two right triangles when we will draw a single altitude in a triangle. Then, prove that both the triangles are congruent. Use the property of congruence to find the distance from one vertex of the triangle to the point where the altitude cuts the side. Then, use Pythagoras theorem to find the length of altitude.

Complete step-by-step answer:
Let $AD$ be the altitude from vertex $A$
We will first draw the corresponding figure.

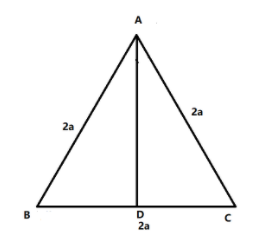
We know that $AD \bot BC$, hence we have two right triangles, $\vartriangle ADB$ and $\vartriangle ADC$
We will now these two triangles congruent.
In $\vartriangle ADB$ and $\vartriangle ADC$
We have $AB = AC$ as they are sides of the equilateral triangle and are equal.
Also, $AD = AD$ is common in both the triangles.
Next, $\angle ADB = \angle ADC$ as both the angles are right angles.
Therefore, by RHS congruency, both the triangles are congruent.
$\vartriangle ADB \cong \vartriangle ADC$
As we know that the corresponding parts of congruent triangles are equal.
Hence, $BD = DC$
Also, $BD + DC = 2a$
Then,
 $
  BD + BD = 2a \\
   \Rightarrow 2\left( {BD} \right) = 2a \\
   \Rightarrow BD = a \\
$
We can now find the length of altitude using Pythagoras theorem.
Pythagoras theorem states that, ${\text{Hypotenus}}{{\text{e}}^2} = {\text{perpendicula}}{{\text{r}}^{\text{2}}}{\text{ + bas}}{{\text{e}}^{\text{2}}}$
On applying Pythagoras theorem in $\vartriangle ADB$, we get,
${\left( {AB} \right)^2} = {\left( {AD} \right)^2} + {\left( {BD} \right)^2}$
On substituting the values of $AB$ and $BD$, we get,
$
  {\left( {2a} \right)^2} = {\left( {AD} \right)^2} + {\left( a \right)^2} \\
   \Rightarrow 4{a^2} = {\left( {AD} \right)^2} + {a^2} \\
   \Rightarrow {\left( {AD} \right)^2} = 3{a^2} \\
   \Rightarrow AD = \sqrt 3 a \\
 $
In an equilateral triangle, the length of all the altitudes is equal.
 Therefore, the length of each altitude of an equilateral triangle with side $2a$ is $\sqrt 3 a$
Hence, option A is correct.

Note: Students are required to know the properties of an equilateral triangle. In this question, after finding the length of the $BD$, we can also trigonometry to find the length of an altitude. That is, in $\vartriangle ADB$ we have$\angle ADB = {60^ \circ }$ as all angles in an equilateral triangles are equal. Then, we get,
$
  \tan {60^ \circ } = \dfrac{{AD}}{a} \\
   \Rightarrow \sqrt 3 = \dfrac{{AD}}{a} \\
   \Rightarrow AD = \sqrt 3 a \\
$