Question

Let A, B be the centers of two circles of equal radii; draw them so that each one of them passes through the centre of the other. Let them intersect at C and D. Examine whether \[\overline {AB} \] and \[\overline {CD} \] are at right angles.

Answer 1

Hint: Here, draw the figure with conditions given in question. Join AB and CD and measure the angle between AB and CD. We can also use congruent triangles concept to check whether \[\overline {AB} \] and \[\overline {CD} \] are at right angles or net.

Complete step-by-step answer:
Given that two circles have equal radii.
Draw two circles of equal radii taking A and B as their centre such that one of them passes through the centre of the other. They intersect at C and D. Join AB and CD.

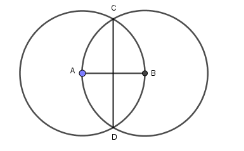
By measurement we can see that \[\overline {AB} \] and \[\overline {CD} \] are at right angles.

Theoretical Proof:
Join AC and BC and mark the intersection of AB and CD as E.

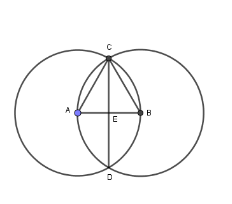
In triangles AEC and BEC,
 $ \Rightarrow $ AC = CB [Radius are equal]
 $ \Rightarrow $ CE = CE [Common in both triangles]
 $ \Rightarrow $ AE = EB [By construction]
By SSS, AEC is congruent to BEC
 $ \Rightarrow $ ∠ AEC = ∠ BEC = 90° [By CPCT]
So, \[\overline {AB} \] and \[\overline {CD} \] are at right angles.

Note: In these types of questions, always draw a rough figure while solving these types of problems. Simply you can measure like 90° or 180°. These types of questions are basically based on construction, so using proper geometrical instruments you can draw the figure and measure the angles or sides, asked in question.
Alternatively, you can prove using triangle properties and similar triangles concepts.
But here you are asked to examine angle so measurement using a protractor will be useful.
Using measurement we can see that in figure AB and CD are perpendicular bisectors of each other.