Question

Let A and B be two sets in the universal set. Then $ A - B $ equals
\[
  A.\,\,A \cap {B^1} \\
  B.\,\,{A^1} \cap B \\
  C.\,\,A \cap B \\
  D.\,\,None\,\,of\,\,these \\
 \]

Answer 1

Hint: For this given problem we first draw a Venn diagram of given sets inside a universal set. Then discussing various or different parts formed to get the required answer to the given problem and hence we will have the correct option out of given options.

Complete step-by-step answer:
Let U be the universal set for two given sets A and B.
Since it is required to find the set or value of $ A - B $ .
We consider that there are some elements common in set A and B.
We can calculate the value of the required set by using the Venn diagram.
For this we draw Venn diagrams for given sets in universal set U. Shown below,

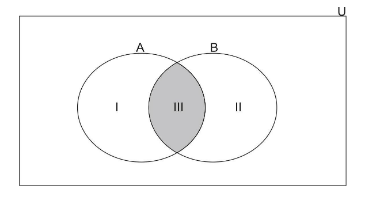
From the above Venn diagram we clearly see that there are three regions formed. To find the answer to a given problem. We discuss different case forms.
Region (iii) in the above Venn diagram is a common region in both set A and B.
There it can be given as set $ A \cap B $
Therefore, option (C) is an incorrect option.
Now, region (ii) is a region which will have only elements which are only in B not in any other set or we can say this part as only B.
Its values can be given as: difference of set B and intersection of two sets. Which is written as:
 $ \Rightarrow n(B) - n(A \cap B) $
Above set also has the same value as $ n(B - A) $ and we see that elements of this set are not common with A.
Therefore, we can also write it as:
 $ \Rightarrow n\left( {B \cap {A^1}} \right)\,\,or\,\left( {{A^1} \cap B} \right) $ = $ n\left( {B - A} \right) $
Hence, option (B) is an incorrect option.
Now, we will discuss region (i).
In this region there are only elements which are in A but not common with any other set.
So, we can say this region as only A.
We can calculate this region or set as the difference of set A and intersection of set A and B.
Hence, given as:
 $ \Rightarrow n\left( A \right) - n\left( {A \cap B} \right) $
Since, this region has elements not common with B. Therefore, we can also write it as:
 $ n\left( {A \cap {B^1}} \right)\,\,or\,\,n\left( {A - B} \right) $
Hence, we see that the correct option is (A).
So, the correct answer is “Option A”.

Note: We can solve this type of set theory problems in two ways. If problem in numeric then we can solve answer by calculating values of different sets by using concept of set theory, but if problem is theoretical then we can use concept of Venn diagram to find value of given set or correct option of given problem.