Question

Let (− 3, 2) be one end of a diameter of a circle with centre (4, 6). Find the other end of the diameter.
A. (11, 10)
B. (10, 2)
C. (1, 1)
D. (7, 5)

Answer 1

Hint: Here, we have coordinates of the centre of the circle and one endpoint of diameter. Centre of a circle exists exactly between the endpoints of its diameter. Assume coordinates of other end of diameter as (x, y) and apply, and apply the midpoint formula to get values of x and y.

Complete step-by-step answer:
 In these types of questions, draw figures on the basis of information given. All diameters of a circle are equal in length and the centre of the circle is mid-point of the diameter.
Let A (− 3, 2) and B (x, y) be the other end of the diameter. And O (4, 6) be the centre of the circle. So, O is the midpoint of AB.

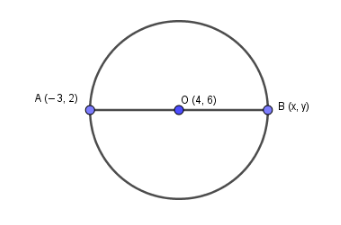
Applying midpoint formula,
$\dfrac{{ - 3 + x}}{2} = 4,\dfrac{{2 + y}}{2} = 6$
⇒ − 3 + x = 8, 2 + y = 12
⇒ x = 11, y = 10
So, B (11, 10)

So, the correct answer is “Option A”.

Note: Alternatively, draw a circle on graph paper with centre (4, 6) and radius is such that it passes through (− 3, 2). Draw a line passing through (− 3, 2) and (4, 6) i.e., centre of the circle which cuts the circle at a point which is the other end of the diameter. See that point on the graph and mention its x and y coordinates. But graphical method is possible for circles of small radius, for circles of large radius algebraic method is used. Coordination geometry basic concepts must be known to solve these types of questions.