Question

Length of the string tied to two rigid supports is \[40\,{\text{cm}}\]. Maximum wavelength (in cm) of a stationary wave produced on it is
A.20
B.80
C.40
D.120

Answer 1

Hint: Recall the concept of the stationary waves formed on a string. Check which type of stationary wave formed on the string will have the maximum wavelength. The length of the wave formed on the string will have length in terms of its wavelength equal to length of the string. Substitute the value of length of string and determine this maximum wavelength of the stationary wave formed.

Complete step by step answer:
We have given that a string is tied to a rigid support with its length \[40\,{\text{cm}}\].
\[L = 40\,{\text{cm}}\]
The stationary wave produced on the string will be maximum when there are two nodes at the points where the ends of the string are tied and one antinode in the middle of the string.
The diagram for the stationary wave with maximum wavelength formed on the string is as follows:

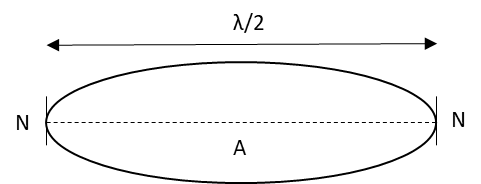
The wavelength of this wave formed is \[\lambda \].
One complete standing stationary wave consists of three nodes and two antinodes.
Since the stationary wave formed on the string has two nodes and one antinode at the middle, it must be a half wave.
Hence, the length of the wave formed on the string must be \[\dfrac{\lambda }{2}\].
As the whole length of the string comprises this half standing wave, the length of the string must be equal to the length of the stationary wave formed on the string.
\[L = \dfrac{\lambda }{2}\]
Rearrange the above equation for wavelength \[\lambda \] of the wave formed on the string.
\[ \Rightarrow \lambda = 2L\]
Substitute \[40\,{\text{cm}}\] for \[L\] in the above equation.
\[ \Rightarrow \lambda = 2\left( {40\,{\text{cm}}} \right)\]
\[ \Rightarrow \lambda = 80\,{\text{cm}}\]
Therefore, the maximum wavelength of the stationary wave produced on the string will be \[80\,{\text{cm}}\].

So, the correct answer is “Option C”.

Note:
The students should keep in mind that the stationary wave formed on the string consists of two nodes and one antinode. Hence, the wave formed on the string is only half of the total wave. Hence, the students should equate the length of string with half of wavelength of the wave and not with the total wavelength of the wave.