Question

What is the length of the shortest side of the \[{30^ \circ } - {60^ \circ } - {90^ \circ }\] triangle if its hypotenuse is $6$?
(a) $3$
(b) $5$
(c) Cannot be determined
(d) None of these

Answer 1

Hint: The given problem revolves around the concepts of geometry of finding the lengths (also, known as mensuration). We will find the required length(s) of the triangle ‘ABC’ by using the trigonometric terms, say, ‘$\sin $’ as we have given the respective hypotenuse of the triangle, to obtain the desired solution.

Complete step-by-step answer:
Since, we have given that
The given triangle is \[{30^ \circ } - {60^ \circ } - {90^ \circ }\] respectively.
As a result, we will consider the figure ABC which resembles the given condition that is given below,

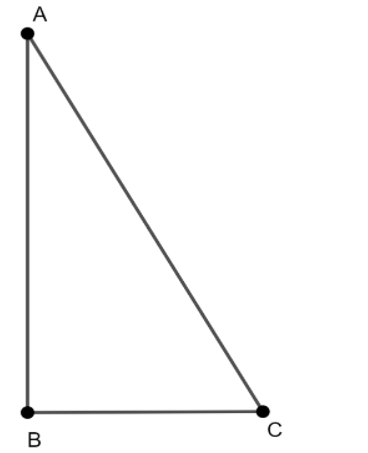
Hence, angle ‘B’ is \[\angle B = {90^ \circ }\] respectively,
So, let us assume that (any)
Remaining angles become (that is ‘A’ and ‘C’ respectively),
$\angle A = {30^ \circ }$
And,
$\angle C = {60^ \circ }$
From figure,
$\therefore $AC is the hypotenuse of the \[{30^ \circ } - {60^ \circ } - {90^ \circ }\] right-angled triangle ‘ABC’ respectively.
But, since we have given that
Hypotenuse, AC $ = 6$ (units)
Hence, we can find the remaining lengths that are ‘AB’ and ‘BC’ respectively by using the Pythagorean Theorem (as the triangle is right angled triangle) which states that “square of hypotenuse is equal to the square of remaining two that is opposite and adjacent sides.”
Mathematically, it is expressed as
$A{C^2} = A{B^2} + B{C^2}$
Also, we can find required lengths or side(s) of the right angled triangle by using the certain trigonometric terms such as ‘$\sin $’, ‘$\cos $’, ‘$\tan $’, etc.
In this case, we will use the second condition to find both the sides (since, we know only one side out of three)
As a result, using ‘$\sin $’ term that is
\[\sin \theta = \dfrac{{opposite{\text{ }}side}}{{hypotenuse}}\]
Say, for angle ${30^ \circ }$
Considering $\angle BAC = {30^ \circ }$ i.e. $\theta = {30^ \circ }$,
$\sin {30^ \circ } = \dfrac{{BC}}{{AC}}$
We know that,
Trigonometric formulae for standard angles ${0^ \circ },{30^ \circ },{45^ \circ },{60^ \circ },{90^ \circ },{180^ \circ },{270^ \circ },{360^ \circ }$ such as, $\sin {30^ \circ } = \dfrac{1}{2}$, etc.
Substituting the values in the above equation, we get
$\therefore \dfrac{1}{2} = \dfrac{{BC}}{6}$
Solving the equation mathematically, we get
$\dfrac{6}{2} = BC$
$BC = 3$ units … (i)
Now, hence we can find the other side i.e. ‘AB’ by using the Pythagoras Theorem $A{C^2} = A{B^2} + B{C^2}$, we get
${6^2} = A{B^2} + {3^2}$
$36 = A{B^2} + 9$
Solving the equation algebraically, we get
$36 - 9 = A{B^2}$
$25 = A{B^2}$
Taking the square roots on the above equation, we get
$AB = 5$ units … (ii)
$\therefore $From (i) and (ii), we have all the lengths for the triangle ABC $\vartriangle ABC$ when hypotenuse, $AC = 6{\text{ }}units$ i.e.
$AB = 5{\text{ }}units$
$BC = 3{\text{ }}units$
Hence, from the above calculations it seems that
The shortest side of the given \[{30^ \circ } - {60^ \circ } - {90^ \circ }\] triangle is $3{\text{ }}units$ respectively.
$\therefore \Rightarrow $Option (a) is correct.
So, the correct answer is “Option a”.

Note: In these cases, we can find the required values by using different methods such as Pythagoras Theorem i.e. $A{C^2} = A{B^2} + B{C^2}$ having its hypotenuse and other means of solving with the help of trigonometric terms such as ‘$\sin $’, ‘$\cos $’, ‘$\tan $’, etc. for the various standard angles such as \[{0^ \circ },{30^ \circ },{45^ \circ },{60^ \circ },{90^ \circ },{180^ \circ },{270^ \circ },{360^ \circ }\] respectively, so as to be sure of our final answer.