Question

Length of the shadow of a 15 meters high pole is $ 5\sqrt 3 $ meters at 7’O clock in the morning. Then what is the angle of elevation of the Sun rays with the ground at that time?

Answer 1

Hint: Here, draw a figure based on the statements given in question. Assume θ as the angle of elevation, and apply the ratio of tan θ. Compare the value of tan θ obtained with standard angle, and find the angle of elevation.

Complete step-by-step answer:
For applying trigonometric methods and standard values one angle of the triangle must be equal to 90°. Also the perpendicular and base of a triangle depends on angle, but hypotenuse remains fixed as this is the side opposite to 90°. In above problem, for ∠ C, base is BC and perpendicular is AB; but for ∠ A, base is AB and perpendicular is BC.
 Let AB be the pole of height 15 m and BC be the shadow of the pole of length $ 5\sqrt 3 $ m.
Let θ be the angle of elevation of the Sun rays with the ground.

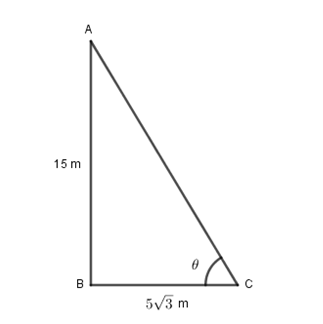
In triangle ABC,
For ∠ θ, Base = BC and Height = AB.
$ \tan \theta = \dfrac{{AB}}{{BC}} = \dfrac{{15m}}{{5\sqrt 3 m}} = \dfrac{3}{{\sqrt 3 }} = \sqrt 3 $
$ \Rightarrow $ tan θ = tan 60°
$\Rightarrow θ = 60° $ [tan 60° = √3]
Hence, the angle of elevation of the Sun rays with the ground is 60°.

Note: In these types of questions, always draw the rough figure to understand the question geometrically. Use trigonometric ratio as per convenience, i.e., first see which sides are given in question and use that trigonometric tool which includes both the sides. Here in this question, we can see that base and perpendicular are given with respect to angle; so we use here tan θ or cot θ.