
Length of the normal chord of the parabola ${{y}^{2}}=8x$ at the point where abscissa and ordinate are equal is:
A.13
B.8
C.$10\sqrt{5}$
D.4
Answer
610.5k+ views
Hint: Take the focal chord as PQ. Their coordinates are of the form $\left( a{{t}^{2}},2at \right)$ . From the given equation of parabola and focal chord concept, we need to get the value of a, ${{t}_{1}}$ and ${{t}_{2}}$ . As abscissa of ordinate are equal, y=x puts that in the equation of parabola. Get value of P & Q, using distance formula. Find length or PQ.
Complete step-by-step answer:
We have been given the equation of parabola as \[{{y}^{2}}=8x\] .
First let us draw the parabola \[{{y}^{2}}=8x\]
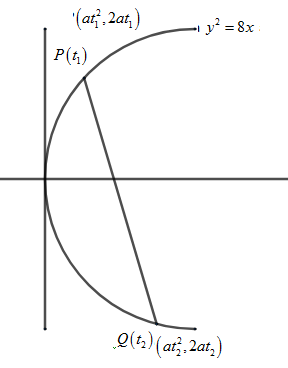
We know the general equation of a parabola as ${{y}^{2}}=4ax$ , Now let us compare both the general equation and the given equation of parabola.
From that we get, latus rectum $4a=8$
$\begin{align}
& a=\dfrac{8}{4}=2 \\
& \text{i}\text{.e}\text{. }a=2 \\
\end{align}$
Let us take the two points on the parabola as $P\left( {{t}_{1}} \right)$ and $Q\left( {{t}_{2}} \right)$ . we know the relation ${{t}_{1}}{{t}_{2}}=-1$ .
Similarly we know that ${{t}_{2}}=-{{t}_{1}}-\dfrac{2}{{{t}_{1}}}$ .
It is said that the abscissa and ordinates are equal, the coordinates are equal so put y=x.
${{y}^{2}}=8x$
So, ${{x}^{2}}=8x\Rightarrow {{x}^{2}}-8x=0$ .
$x\left( x-8 \right)=0$ Hence $x=0$ or $x-8=0$
i.e. x can be either 0 or 8. So when x=8, y=8
Thus we got the coordinate of $\left( x,y \right)$ as $\left( 8,8 \right)$ .
We can take the coordinate of $P\left( at_{1}^{2},2a{{t}_{1}} \right)$ and $Q\left( at_{2}^{2},2a{{t}_{2}} \right)$ .
Thus we got a=2, So, \[~P\left( 2t_{1}^{2},4{{t}_{1}} \right)\] and $Q\left( 2t_{2}^{2},4a{{t}_{2}} \right)$ .
Now we get the coordinate of $\left( x,y \right)=\left( 8,8 \right)$ and coordinate \[\left( 2t_{1}^{2},4{{t}_{1}} \right)\] .
Now let us equate the x and y coordinates of both.
Thus,
$\begin{align}
& 4{{t}_{1}}=8 \\
& {{t}_{1}}=\dfrac{8}{4}=2 \\
\end{align}$
Thus we got ${{t}_{1}}=2$
We know that ${{t}_{2}}=-{{t}_{1}}-\dfrac{2}{{{t}_{1}}}=-2-\dfrac{2}{2}=-2-1=-3$
Thus ${{t}_{2}}=-3$ .
Thus let us put ${{t}_{1}}=2$ and ${{t}_{2}}=-3$ in the coordinate of P and Q
\[\begin{align}
& ~P\left( 2t_{1}^{2},4{{t}_{1}} \right)=P\left( 2\times {{2}^{2}},4\times 2 \right)=P\left( 8,8 \right) \\
& Q\left( 2t_{2}^{2},4a{{t}_{2}} \right)=Q\left( 2\times {{\left( -3 \right)}^{2}},4\times -3 \right)Q\left( 18,-12 \right) \\
\end{align}\]
Now, let us find the length of normal chord PQ using distance formula
distance$\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$
Put $\left( {{x}_{1}},{{y}_{1}} \right)=\left( 8,8 \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)=\left( 18,12 \right)$
Length of normal chord PQ $=\sqrt{{{\left( 18-8 \right)}^{2}}+{{\left( -12-8 \right)}^{2}}}$
\[=\sqrt{{{10}^{2}}+{{\left( -20 \right)}^{2}}}=\sqrt{100+400}=\sqrt{500}=\sqrt{100\times 5}=10\sqrt{5}\] .
Hence we got the length of a normal chord as $10\sqrt{5}$ .
Therefore, option (C) is the correct answer.
Note: The normal at the point \[\left( 2t_{1}^{2},4{{t}_{1}} \right)\] meets the parabola again in the point $\left( 2t_{2}^{2},4a{{t}_{2}} \right)$ , thus ${{t}_{2}}=-{{t}_{1}}-\dfrac{2}{{{t}_{1}}}$ . We may sometimes take ${{t}_{1}}{{t}_{2}}=-1$ , but that is not concept to use and it will give us wrong values of ${{t}_{1}}$ and ${{t}_{2}}$ .
Complete step-by-step answer:
We have been given the equation of parabola as \[{{y}^{2}}=8x\] .
First let us draw the parabola \[{{y}^{2}}=8x\]
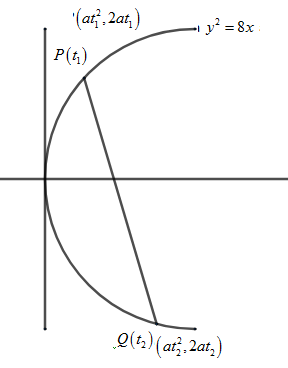
We know the general equation of a parabola as ${{y}^{2}}=4ax$ , Now let us compare both the general equation and the given equation of parabola.
From that we get, latus rectum $4a=8$
$\begin{align}
& a=\dfrac{8}{4}=2 \\
& \text{i}\text{.e}\text{. }a=2 \\
\end{align}$
Let us take the two points on the parabola as $P\left( {{t}_{1}} \right)$ and $Q\left( {{t}_{2}} \right)$ . we know the relation ${{t}_{1}}{{t}_{2}}=-1$ .
Similarly we know that ${{t}_{2}}=-{{t}_{1}}-\dfrac{2}{{{t}_{1}}}$ .
It is said that the abscissa and ordinates are equal, the coordinates are equal so put y=x.
${{y}^{2}}=8x$
So, ${{x}^{2}}=8x\Rightarrow {{x}^{2}}-8x=0$ .
$x\left( x-8 \right)=0$ Hence $x=0$ or $x-8=0$
i.e. x can be either 0 or 8. So when x=8, y=8
Thus we got the coordinate of $\left( x,y \right)$ as $\left( 8,8 \right)$ .
We can take the coordinate of $P\left( at_{1}^{2},2a{{t}_{1}} \right)$ and $Q\left( at_{2}^{2},2a{{t}_{2}} \right)$ .
Thus we got a=2, So, \[~P\left( 2t_{1}^{2},4{{t}_{1}} \right)\] and $Q\left( 2t_{2}^{2},4a{{t}_{2}} \right)$ .
Now we get the coordinate of $\left( x,y \right)=\left( 8,8 \right)$ and coordinate \[\left( 2t_{1}^{2},4{{t}_{1}} \right)\] .
Now let us equate the x and y coordinates of both.
Thus,
$\begin{align}
& 4{{t}_{1}}=8 \\
& {{t}_{1}}=\dfrac{8}{4}=2 \\
\end{align}$
Thus we got ${{t}_{1}}=2$
We know that ${{t}_{2}}=-{{t}_{1}}-\dfrac{2}{{{t}_{1}}}=-2-\dfrac{2}{2}=-2-1=-3$
Thus ${{t}_{2}}=-3$ .
Thus let us put ${{t}_{1}}=2$ and ${{t}_{2}}=-3$ in the coordinate of P and Q
\[\begin{align}
& ~P\left( 2t_{1}^{2},4{{t}_{1}} \right)=P\left( 2\times {{2}^{2}},4\times 2 \right)=P\left( 8,8 \right) \\
& Q\left( 2t_{2}^{2},4a{{t}_{2}} \right)=Q\left( 2\times {{\left( -3 \right)}^{2}},4\times -3 \right)Q\left( 18,-12 \right) \\
\end{align}\]
Now, let us find the length of normal chord PQ using distance formula
distance$\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$
Put $\left( {{x}_{1}},{{y}_{1}} \right)=\left( 8,8 \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)=\left( 18,12 \right)$
Length of normal chord PQ $=\sqrt{{{\left( 18-8 \right)}^{2}}+{{\left( -12-8 \right)}^{2}}}$
\[=\sqrt{{{10}^{2}}+{{\left( -20 \right)}^{2}}}=\sqrt{100+400}=\sqrt{500}=\sqrt{100\times 5}=10\sqrt{5}\] .
Hence we got the length of a normal chord as $10\sqrt{5}$ .
Therefore, option (C) is the correct answer.
Note: The normal at the point \[\left( 2t_{1}^{2},4{{t}_{1}} \right)\] meets the parabola again in the point $\left( 2t_{2}^{2},4a{{t}_{2}} \right)$ , thus ${{t}_{2}}=-{{t}_{1}}-\dfrac{2}{{{t}_{1}}}$ . We may sometimes take ${{t}_{1}}{{t}_{2}}=-1$ , but that is not concept to use and it will give us wrong values of ${{t}_{1}}$ and ${{t}_{2}}$ .
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

10 examples of friction in our daily life




