Question

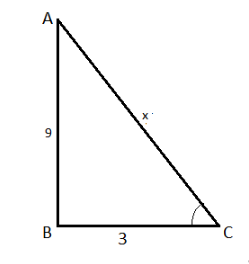
What is the length of the hypotenuse of a right triangle if the two other sides are of lengths $ 3 $ and $ 9 $ ?

Answer 1

Hint: Here, first of all we will assume the unknown side, the length of the hypotenuse to be “x” and draw the diagram. by using the Pythagoras theorem which states that the sum of the squares of the right angled triangle is equal to the third side.

Complete step-by-step answer:
Let us assume the length of the hypotenuse be “x”
 $ {(3)^2} + {(9)^2} = {x^2} $
Now, to find the value of “x” using Pythagoras theorem which states that the sum of square of opposite side and the square of an adjacent side is equal to the square of hypotenuse.

The above expression can be re-written as –
 $ {x^2} = {(3)^2} + {(9)^2} $
Simplify the above expression –
 $ {x^2} = 9 + 81 $
Add the terms on the right hand side of the equation –
 $ {x^2} = 90 $
Take the square root on both the sides of the equation –
 $ \sqrt {{x^2}} = \sqrt {90} $
Square and square-root cancel on the right hand side of the equation –
 $ x = \sqrt {9 \times 10} $
Simplify finding the root of the possible terms
 $ x = 3\sqrt {10} $ units
Hence, the measure of the hypotenuse is $ 3\sqrt {10} $ units.
So, the correct answer is “ $ 3\sqrt {10} $ units”.

Note: Always remember that the measure of the side of the triangle can never be zero nor negative. Be good in squares and square-root concepts and apply wisely. Hypotenuse is the longest side in any right angled triangle.