Question

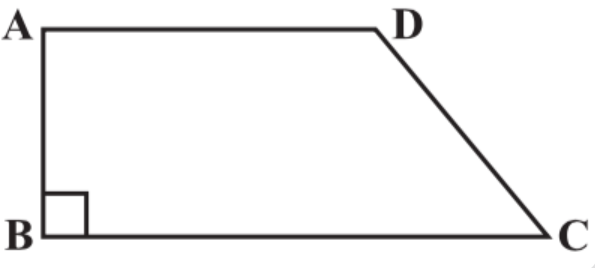
Length of the fence of a trapezium shaped field $ABCD$ is $120m$. If $BC = 48m,CD = 17m$ and $AD = 40m$, find the area of this field. Side $AB$ is perpendicular to the parallel sides $AD$ and $BC$.

Answer 1

Hint: Find the remaining side of the trapezium and then use the formula for area of trapezium i.e. Area of trapezium $ = \dfrac{1}{2} \times $(Sum of parallel sides) $ \times $(Distance between parallel sides).

Complete step-by-step answer:
According to the question, the length of fence of the field is $120m$. Then we have:
$ \Rightarrow AB + BC + CD + AD = 120$
Given, $BC = 48m,CD = 17m$ and $AD = 40m$. We can find $AB$:
$
   \Rightarrow AB + 48 + 17 + 40 = 120, \\
   \Rightarrow AB = 120 - 105, \\
   \Rightarrow AB = 15m \\
$
We know that:
Area of trapezium $ = \dfrac{1}{2} \times $(Sum of parallel sides) $ \times $(Distance between parallel sides).
As we can see from the figure, parallel sides are $AD$ and $BC$ and the distance between them is $AB$. So, area of trapezium $ABCD$ is:
$
   \Rightarrow A = \dfrac{1}{2} \times \left( {AD + BC} \right) \times AB, \\
   \Rightarrow A = \dfrac{1}{2} \times \left( {40 + 48} \right) \times 15, \\
   \Rightarrow A = \dfrac{1}{2} \times 88 \times 15, \\
   \Rightarrow A = 44 \times 15, \\
   \Rightarrow A = 660{m^2} \\
$
Therefore the area of the field is $660{m^2}$
Note: If we drop a perpendicular from point $D$ on $BC$, the above figure will be divided into two smaller figures of a rectangle and a triangle. We can calculate their separate areas and add them to get the overall area. This method can also be used to solve the question.