Question

What length of tarpaulin 3-meter-wide will be required to make a conical tent of height 8 metre and base radius 6 metre? Assume that the excellent material will be required for stitching margins and wastage in cutting is approximately 20 centimetres.

Answer 1

Hint: For solving this problem, first we calculate the curved surface area of the conical tank. Now, the area of tarpaulin material should be equal to the curved surface area of the conical tank. We are given the width of tarpaulin. By using the area formula, we can evaluate the length.

Complete step by step answer:

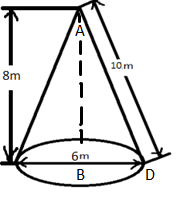
The curved surface area of the cone is the sum of the area of the top slant surface. Therefore, the total surface area can be expressed as: $\pi rl\ldots (1)$.
According to the problem statement we are given that the radius of tent is 6m and the height is 8m. For calculating the curved surface area, we required the slant length. To evaluate the slant length, we use Pythagoras theorem $\left( {{a}^{2}}+{{b}^{2}}={{c}^{2}} \right)$ which can be stated as:
$\begin{align}
  & A{{B}^{2}}+B{{D}^{2}}=A{{D}^{2}} \\
 & {{6}^{2}}+{{8}^{2}}=A{{D}^{2}} \\
 & AD=\sqrt{36+64} \\
 & AD=\sqrt{100} \\
 & AD=10m \\
\end{align}$
Therefore, the slant length is 10m.
Now, putting this data in equation 1 we get,
$\begin{align}
  & C.S.A=\pi \times 6\times 10 \\
 & C.S.A=60\pi {{m}^{2}} \\
\end{align}$
Also, the width of the tarpaulin is 3m. Let the length of the tarpaulin be L. Therefore, the area of tarpaulin is the area of rectangle: $3\times L$
Since, the curved surface area of the conical tank is equal to the area of tarpaulin. So, the length of tarpaulin can be expressed as:
$\begin{align}
  & 3\times L=60\pi \\
 & L=\dfrac{60\pi }{3} \\
 & L=62.8312 \\
 & L\approx 62.8m \\
\end{align}$
Also, the wastage is approximately 20 cm. This must be added to obtain the final length.

So, the final length of tarpaulin required is 62.8 + 0.2 = 63 m.

Note: Students must be careful while calculating the final length of tarpaulin. Common mistake is the ignorance of wastage of tarpaulin given in the question. It must be added after converting into a suitable unit to obtain the final length of the tarpaulin.