Question

What is the length of a diagonal of a square if its area is 98 square feet?

Answer 1

Hint: We know that all the sides of a square are equal to each other, and all angles are right angles. Also, the area of square can be written as $A={{a}^{2}}=\dfrac{{{d}^{2}}}{2}$, where a is the edge length and d is the length of diagonal.

Complete step by step solution:
We know that a square is a rectangle in which the adjacent sides are equal to one another. Hence, we can say that all the sides of a square are equal.
Also, we know that all the interior angles of a square are a right angle.
We have shown the figure of a square ABCD below, with the length of sides equal to a and the length of diagonal AC = ${{d}_{1}}$ and the diagonal BD = ${{d}_{2}}$.

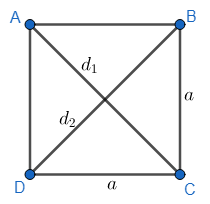
We know that the area of square can be written as,
$A=a\times a$
And thus, the area is $A={{a}^{2}}...\left( i \right)$
Now, since the interior angles of the square are right angles, we can use the Pythagoras theorem. Hence, we can write
${{d}_{1}}^{2}={{a}^{2}}+{{a}^{2}}$
Thus, we can write
${{d}_{1}}^{2}=2{{a}^{2}}$
On taking square roots on both sides, we can write
${{d}_{1}}=\sqrt{2}a$
Similarly, we can write for another diagonal as well,
${{d}_{2}}^{2}={{a}^{2}}+{{a}^{2}}$
Thus, we get
${{d}_{2}}^{2}=2{{a}^{2}}$
And, on taking square roots, we get
${{d}_{2}}=\sqrt{2}a$
Thus, we can write
${{d}_{1}}\times {{d}_{2}}=2{{a}^{2}}$
Or, we get
${{a}^{2}}=\dfrac{1}{2}\left( {{d}_{1}}\times {{d}_{2}} \right)$
So, now putting the value of ${{a}^{2}}$ in equation (i), we get
$A=\dfrac{1}{2}\left( {{d}_{1}}\times {{d}_{2}} \right)$
But we know that, in a square, the length of each diagonal is equal to each other, as seen above.
Hence, we can write
$A=\dfrac{{{d}^{2}}}{2}...\left( ii \right)$
Here, in this question, we are given that $A=98$, and thus we have
$98=\dfrac{{{d}^{2}}}{2}$
We can write this equation as
${{d}^{2}}=2\times 98$
Or, ${{d}^{2}}=196$
On taking square roots on both sides, we get
$d=14$.
Hence, the length of diagonal is 14 feet.

Note: We must know that each square is also a rectangle, and each square is also a rhombus or a parallelogram. Hence, we have used the properties of rectangle and rhombus. Also, we must note that we have neglected the value -14, as the length can never be a negative value.