Question

What is the length, in feet, of the hypotenuse of a right-angled triangle with the length of its perpendicular sides as $6$ feet long and $7$ feet, respectively?
A.$\sqrt {13} $
B.$\sqrt {85} $
C.$13$
D.$21$
E.$42$

Answer 1

Hint: In order to find the length of the hypotenuse of a right-angled triangle, first construct the rough diagram of a right- angled triangle, mention the given parts and by using the Pythagoras theorem, find the length of the hypotenuse.

Complete answer:
 We are given with a right-angled triangle whose length of the perpendicular sides are as $6$ feet long and $7$ feet.
Constructing a rough diagram of a right- angled triangle named ABC having ${90^ \circ }$ angle at B and mentioning the sides:

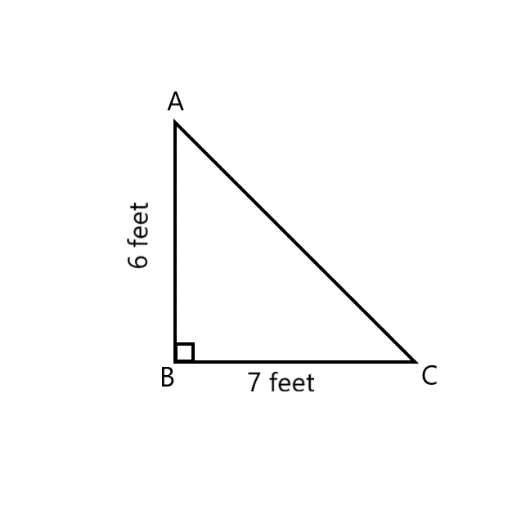
Since, it is given two perpendicular sides, so we have considered one side to be the perpendicular and another to be the base.
As it is a right- angled triangle, we can use the pythagorean theorem to find the hypotenuse of the triangle. The Pythagoras theorem states that the sum of the squares of the perpendiculars is equal to the square of the hypotenuse.
So, according to this, we can write:
$A{B^2} + B{C^2} = A{C^2}$ …………(1)
From the figure, we have:
$
  AB = 6 \\
  BC = 7 \\
 $
Substituting these values in the equation 1 and we get:
$ \Rightarrow {\left( 6 \right)^2} + {\left( 7 \right)^2} = A{C^2}$
Solving the values, we get:
$ \Rightarrow 36 + 49 = A{C^2}$
$ \Rightarrow 85 = A{C^2}$
Taking square root both the sides:
$ \Rightarrow \sqrt {85} = \sqrt {A{C^2}} $
$ \Rightarrow \sqrt {A{C^2}} = \sqrt {85} $
$ \Rightarrow AC = \sqrt {85} $
And, AC was the hypotenuse, so the length of the hypotenuse is $\sqrt {85} $ feet.
Hence, Option B is correct.

Note:
1.We have taken $ \Rightarrow \sqrt {A{C^2}} = AC$ as because we know that ${\left( x \right)^2} = {x^2}$ that implies $\sqrt {{x^2}} = x$, so similarly the value is taken for AC.
2.Pythagoras Theorem is always applied on the right- angled triangle, do not use it in another triangle.