Question

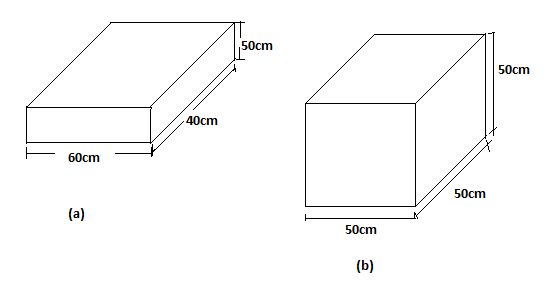
$\left( 1 \right)$ There are two cuboidal boxes as shown in the adjoining figure. Which box requires the lesser amount of material to make?

$\left( 2 \right)$ The suitcase with measures \[80cm \times 48cm \times 24cm\] is to be covered with a tarpaulin cloth. How many meters of tarpaulin of width \[96cm\] required cover \[100\] suitcases?

Answer 1

Hint: $\left( 1 \right)$ First, we want to find the total surface area of each given box and then compare which is the lesser amount of material to make the box.
$\left( 2 \right)$ We have to find the cuboid for the total surface area of the suitcase.
Then, find the area of the tarpaulin to cover the suitcase.
Tarpaulin is the strong material that water cannot pass through, which is used for covering things to protect them from the rain.

Formula used: Total surface area of cuboid = \[2(lb + bh + hl)\] square units
Total surface area of a cube \[ = 6{a^2}\] centimetre square.

Complete step-by-step answer:
$\left( 1 \right)$ First we assume that the material used by the first box is $\left( a \right)$ and the material used by the second box is $\left( b \right)$
Now we have to find out the total surface area of the first box
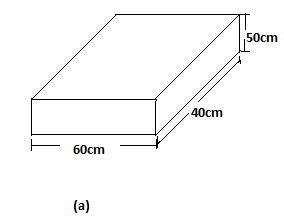
The material used by the first box $\left( a \right)$

Here we can write,
Length=\[60cm\]
Breadth=\[40cm\]
Height=\[50cm\]
Substitute the given data in the formula, we get
Total surface area of cuboid = \[2(lb + bh + hl)\] square units
\[ \Rightarrow 2(60 \times 40 + 40 \times 50 + 50 \times 60)\]
On multiplying the brackets terms we get,
\[ \Rightarrow 2(2400 + 2000 + 3000)\]
Let us add the bracketed terms we get,
\[ \Rightarrow 2(7400)\]
On multiplying
\[ \Rightarrow 14800\]$cm^2$
So, the total surface area of the cuboid $\left( a \right)$is \[14800\] Centimetre square.
Now we have to find out the total surface area of the cube \[\left( b \right)\]
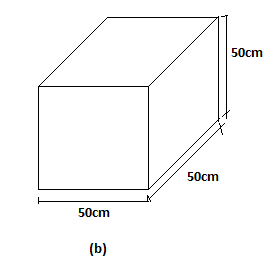
That is, the material used by second box $\left( b \right)$

Here we can write it as,
Length=\[50cm\]
Breadth=\[50cm\]
Height=\[50cm\]
So the box is a cube with sides, $a = 50{\text{ cm}}$
Total surface area of a cube \[ = 6{a^2}\] centimetre square.
Substitute the value of a in the formula we get,
\[ = 6{\left( {50} \right)^2}\]
On squaring the terms we get,
\[ = 6\left( {2500} \right)\]
Let us multiply the terms we get,
\[ = 15000{\text{ c}}{{\text{m}}^2}\]
So, the total surface area of the cube $\left( b \right)$is \[15000\] Centimetre square.
Already we find the total surface area of the cuboid $\left( a \right)$ is \[14800\] Centimetre square.
Here we Say that the total surface area of the box is $\left( a \right)$ lesser than the total area of the box$\left( b \right)$
$\therefore $ The second box $\left( b \right)$ requires more material.
Hence, the first box $\left( a \right)$ requires less amount of material to make.

$\left( 2 \right)$

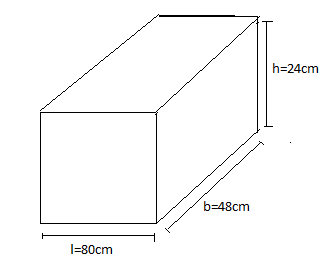
It is given that the suitcase has
Length=\[80cm\]
Breadth=\[48cm\]
Height=\[24cm\]
A tarpaulin cloth covers the suitcase,
Therefore,
Area of cloth to cover in the suitcase = total surface area of cuboid
Total surface area of cuboid = \[2(lb + bh + hl)\]square units
Substitute the given data in the formula we get
 = \[2(80 \times 48 + 48 \times 24 + 24 \times 80)\]
On multiplying,
=\[2(3840 + 1152 + 1920)\]
Let us adding the bracket terms,
 =\[2(6912)\]
Let us multiply the terms
Total surface area of cuboid =\[13824c{m^2}\]= area of one suitcase.
Here we have to find how many meters used to cover \[100\] suitcase
Area of tarpaulin is equal to \[100 \times \] area of one suitcase.
Area of tarpaulin \[ = 100 \times 13824\]
On multiplying we get,
\[ = 1382400\]
Now we have to find out the length of the tarpaulin,
Since, we already have an given that the tarpaulin is a rectangle with width \[ = 96cm\]
Area of tarpaulin \[ = 1382400\]
That is we can write it as,
\[96 \times {\text{length}}\] \[ = 1382400\]
Length \[ = \dfrac{{1382400}}{{96}}\]
On dividing we get,
\[ = 14400\] Centimetre
Now we have to convert into meters so we divide into \[100\]
We can write it as, \[ = 14400 \times \dfrac{1}{{100}}\]
On cancelling the same term we get
\[ = 144\] Meter.
Hence, the length of tarpaulin of width \[96cm\] required cover \[100\] suitcases is \[144m\]

Note: The Material used and suitcase cover both sums depend on the shape of the cuboid.
The cuboid has three dimensions of width, length, depth and six rectangular faces.
All vertices are right angles.