Question

What is the LCM (Least Common Multiple) of \[26{\text{ and 39}}\]?

Answer 1

Hint: We will discuss Least Common Multiple in detail while solving this problem and then solve this problem using those definitions and examples. We will also use the prime factorization method also to solve this problem. Prime numbers are the numbers which have only two divisors.

Complete step by step answer:
In mathematics, the Least Common Multiple (LCM) of two numbers is defined as the least among the common multiples of those two numbers. It can be calculated for two or more numbers.
Now, we have to calculate the LCM of \[26{\text{ and 39}}\].
According to the prime factorization method,
It can be written as,

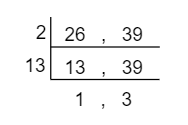
So, \[LCM = 2 \times 13 \times 1 \times 3 = 78\]
Therefore, the Least Common Multiple of 26 and 39 is 78.

Additional information:
Let us now know the method of finding LCM of two numbers.
Let the two numbers be \[6\] and \[15\].
The multiples of 6 are \[6,12,18,24,30,36,42,48,54,60,66,72,......\]
The multiples of 15 are \[15,30,45,60,75,90,105,120,135,150,......\]
When you observe, the multiples that are common for 6 and 15 are \[30,60,90,120,......\]
So, the least one among the common multiples is \[30\].
So, Least Common Multiple of 6 and 15 is 30.
LCM can also be calculated in this way.

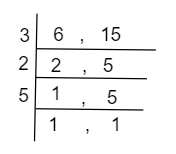
So, \[LCM = 3 \times 2 \times 5 = 30\]
This is the prime factorization method.

Note:
We have to consider the least value among the multiples that we got in common though we got many multiples in common. We can try both methods as per our convenience. But if we have more than two numbers for which we need to find LCM, then the best method is the prime factorization method.
The LCM of two co-primes is equal to the product of those two numbers. Co-primes are the numbers which have only 1 as a common divisor.
For example, LCM of 3 and 4 is 12, which is a product of 3 and 4.