Question

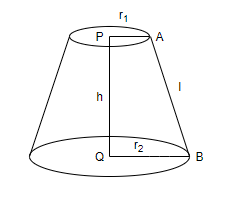
Lateral surface area of the frustum of a cone whose smaller radius is \[{{r}_{2}}\] and larger radius is \[{{r}_{1}}\] is

(a) \[\pi \left( {{r}_{2}}-{{r}_{1}} \right)h\]
(b) \[\pi \left( {{r}_{2}}+{{r}_{1}} \right)h\]
(c) \[\pi \left( {{r}_{2}}-{{r}_{1}} \right)l\]
(d) \[\pi \left( {{r}_{2}}+{{r}_{1}} \right)l\]

Answer 1

Hint: Assume an extension of this frustum in the form of cone. The frustum can be seen as removing the cone with smaller radius from the cone with larger radius. To calculate the lateral surface area of frustum, subtract the lateral surface area of cone with smaller radius from the lateral surface area of cone with larger radius.

Complete step-by-step answer:
We have to find the lateral surface area of the given frustum whose smaller radius is \[{{r}_{1}}\] and larger radius is \[{{r}_{2}}\]. The height of the given frustum is h and slant height is l.
We will assume an extension of the given frustum in the form of a cone. We can get the frustum by removing the cone with smaller radius from the cone with larger radius. Hence, the lateral surface area of frustum is obtained by subtracting the lateral surface area of cone with smaller radius from the lateral surface area of cone with larger radius.
Let’s assume that the frustum is extended as a cone at vertex O. Let’s assume that the height OP of this cone is \[{{h}_{1}}\] and slant height OA is \[{{l}_{1}}\], as shown in the figure.

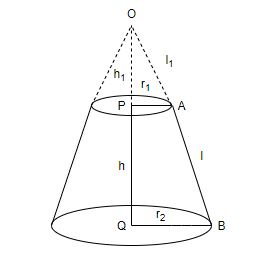
As \[OP\bot PA\] and \[OQ\bot QB\], we observe that PA is parallel to QB. Thus, we have \[\angle OAP=\angle OBQ\]. So, we have \[\cos \left( \angle OAP \right)=\cos \left( \angle OBQ \right).....\left( 1 \right)\]
We will firstly consider the cone formed by the triangle \[\vartriangle OPA\]. The height of this cone is \[{{h}_{1}}\], slant height is \[{{l}_{1}}\] and radius is \[{{r}_{1}}\]. As the cone is right angled at point P, we have \[\cos \left( \angle OAP \right)=\dfrac{base}{hypotenuse}=\dfrac{AP}{OA}=\dfrac{{{r}_{1}}}{{{l}_{1}}}.....\left( 2 \right)\].
Now, we will consider the triangle \[\vartriangle OQB\]. The height of this cone is \[{{h}_{2}}\], slant height is \[{{l}_{2}}\] and radius is \[{{r}_{2}}\]. As the cone is right angled at point Q, we have \[\cos \left( \angle OBQ \right)=\dfrac{base}{hypotenuse}=\dfrac{QB}{OB}=\dfrac{{{r}_{2}}}{{{l}_{1}}+l}.....\left( 3 \right)\].
Substituting equation (2) and (3) in equation (1), we have \[\dfrac{{{r}_{1}}}{{{l}_{1}}}=\dfrac{{{r}_{2}}}{{{l}_{1}}+l}\].
Simplifying the above equation, we have \[{{r}_{1}}\left( l+{{l}_{1}} \right)={{r}_{2}}{{l}_{1}}\].
\[\begin{align}
  & \Rightarrow {{r}_{2}}{{l}_{1}}=l{{r}_{1}}+{{r}_{1}}{{l}_{1}} \\
 & \Rightarrow {{l}_{1}}\left( {{r}_{2}}-{{r}_{1}} \right)=l{{r}_{1}} \\
 & \Rightarrow {{l}_{1}}=\dfrac{l{{r}_{1}}}{{{r}_{2}}-{{r}_{1}}} \\
\end{align}\]
 Thus, we have \[{{l}_{1}}=\dfrac{l{{r}_{1}}}{{{r}_{2}}-{{r}_{1}}}.....\left( 4 \right)\].
We will now calculate the lateral surface area of the frustum. We can find lateral surface area of frustum by subtracting the lateral surface area of cone with smaller radius from cone with larger radius.
We know that the lateral surface area of a cone with radius r and slant height l is \[\pi rl\].
The lateral surface area of cone with radius \[{{r}_{1}}\] and slant height \[{{l}_{1}}\] is \[\pi {{r}_{1}}{{l}_{1}}\].
The lateral surface area of cone with radius \[{{r}_{2}}\] and slant height \[{{l}_{1}}+l\] is \[\pi {{r}_{2}}({{l}_{1}}+l)\].
Thus, the lateral surface area of frustum \[=\pi {{r}_{2}}({{l}_{1}}+l)-\pi {{r}_{1}}{{l}_{1}}\].
We can rewrite the lateral surface of frustum as \[\pi {{l}_{1}}\left( {{r}_{2}}-{{r}_{1}} \right)+\pi l{{r}_{2}}\].
Substituting equation (4) in the above expression, we have the lateral surface area of frustum \[=\pi \left( l{{r}_{1}} \right)+\pi l{{r}_{2}}=\pi l\left( {{r}_{1}}+{{r}_{2}} \right)\].
Hence, the lateral surface area of frustum is \[\pi l\left( {{r}_{1}}+{{r}_{2}} \right)\], where l is the slant height of frustum, \[{{r}_{1}}\] is the smaller radius of frustum and \[{{r}_{2}}\] is the larger radius of frustum, which is option (d).

Note: Frustum is the portion of solid that lies between one or two parallel planes cutting it. A right frustum is a parallel truncation of a right cone. A frustum is circular if it has circular bases. The height of frustum is the perpendicular distance between the planes of two bases. While calculating the lateral surface area of frustum, you can also write the area of frustum in terms of the height and radius. Use sine function to relate height of frustum with the slant height and radius of its two bases.